Биномиальное распределение

Дискретная СВ X распределена по биномиальному закону, если она принимает значения 0, 1, 2, …, n с вероятностями:

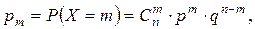(1.33)

где 0 < p < 1, q = 1 – p, m = 0, 1, …, n.

Из схемы Бернулли следует, что СВ X – число появлений события А в серии из n независимых опытов, в каждом из которых событие А может появиться с вероятностью p, имеет биномиальное распределение. Для
СВ X, имеющей биномиальное распределение с параметрами p и n,

M(X) = np, D(X) = npq, (1.34)

где q = 1 – p.

Следует отметить, что гипергеометрическое распределение при n малых по сравнению с N (практически при n < 0,1N) приближается к биномиальному распределению с параметрами n и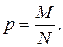

Замечание 1. Для вычисления 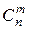при достаточно больших n и m применима формула Стирлинга:

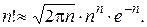
Замечание 2. Для биномиальных вероятностей справедлива рекуррентная формула:

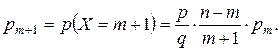
Замечание 3. Наиболее вероятное число успехов K₀ в серии из n независимых испытаний удовлетворяет неравенству:

np – q ≤ K₀ < np + p.

Предельные теоремы

При большом числе испытаний непосредственное вычисление вероятностей P(X = m) и P(m₁ ≤ X ≤ m₂) для СВ X, распределено по биномиальному закону, становится громоздким, так как факториалы, входящие в формулу 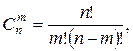будут очень большими числами. В этом случае для вычисления указанных вероятностей можно использовать асимптотические (предельные) формулы.

Когда оба параметра p и q заметно отличны от 0, применяются локальная (1.35, 1.36) и интегральная формулы Муавра-Лапласа (1.38, 1.40).

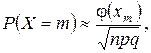(1.35)

где

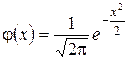(1.36)

– плотность нормированной нормальной СВ X, а

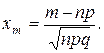(1.37)

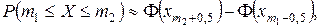(1.38)

где

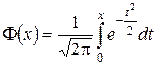(1.39)

– функция Лапласа,

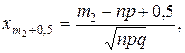
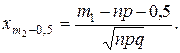(1.40)

Имеются таблицы значений j(x) (таблица 1) и F(x) (npq > 20) (таблица 2).

С помощью этих формул при n ³ 100 и npq > 20, как правило, удается получить искомые вероятности с точностью до трех-четырех знаков после запятой.