Логарифмически нормальное распределение

И в практике наших расчетов и за рубежом довольно часто применяется лога­рифмически нормальное распределение. Подробное изложение тео­ретических основ и приемов практического использования этого закона дается в работах Г. А. Алексеева [2] и Е. Г. Блохинова [9].

Используется две разновидности логарифмически нормального распределения. Первая из них заключается в логарифмическом преобразовании всех членов ряда наблюдений X. При этом, если значения исходного ряда х₁, х₂, x₃, . .., х_п имели область изменения от 0 до ∞ (0 ≤ х <∞) (т. е. ряд заведомо асимметричен, так как изменения ниже среднего значения ограничены 0 (х≥0), а выше – неограничены), то преобразованные значения и=lпх будут уже находиться в пределах от -∞ до ∞ (-∞ < и < ∞), т. е. об­ласть существования будет приближаться к нормальному закону распределения.

Такой подход весьма прост в техническом отношении и обла­дает важным принципиальным достоинством: он позволяет исполь­зовать весь арсенал достаточно хорошо разработанных методиче­ских средств нормального закона, но в то же время подобный подход неудобен тем, что при проведении анализа приходится пользоваться логарифмическим языком. В единицах логарифмов выражаются рассматриваемые величины и соответственно их па­раметры, в логарифмической шкале строится функция обеспеченности и производятся необходимые сопоставления и лишь в конце расчетов итоговые характеристики выражаются в натуральных единицах.

Для построения логарифмически нормальной кривой обеспечен­ности при логарифмическом преобразовании всех членов ряда X необходимо выполнить следующие преобразования:

1) прологарифмировать исходный ряд u_i = ln x_i;

2) рассчитать числовые характеристики ряда логарифмов ис­ходных величин : математическое ожидание

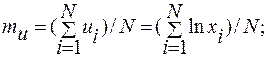(4.64)

среднее квадратичное отклонение

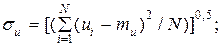(4.65)

3) рассчитать ординаты нормальной кривой обеспеченности по формуле (4.20), где

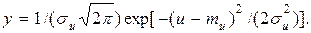(4.66)

Обычно для этого используется таблица значений нормальной кривой обеспеченности t_P = f(P%) ( [64в], прилож. 2, С_s =0). По значениям t_P рассчитываются значения u_pзаданной обеспеченности

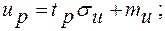(4.67)

и затем определяются действительные значения X

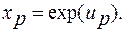(4.68)

В ряде случаев нижний предел значений рассматриваемого ряда X существенно больше нуля. Тогда нижняя граница полу­ченного в результате логарифмирования ряда U будет положи­тельной. Для учета этого обстоятельства предлагается следующее преобразование:

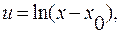(4.69)

где x_о — нижний предел случайной величины X.

Если, как часто бывает в практике, х₀ неизвестно, то при его определении исходят из положения о том, что при соответствую­щем подборе х_о распределение U должно стать симметричным, т. е. значения C_s и μ₃ должны быть равны нулю:

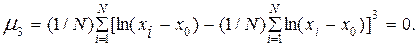(4.70)

Решение уравнения (4.70) обычно производится подбором. Для этого последовательно назначают несколько значений х₀ и для каждого рассчитывают значение μ₃. Затем строят график зави­симости μ₃= f(x_o) и по графику определяют то значение х_o, для которого μ₃ равно или близко к нулю..

Возможны такие ситуации, когда, полученное в результате расчетов, х_о не имеет физического смысла. В этом случае следует или отказаться от использования данного закона распределения, или же при достаточном физическом обосновании назначить при­ближенное значение x_о ≤ х_мин, где х_мин — наблюденное минималь­ное значение X.

Другая разновидность логарифмической модификации исход­ного ряда X заключается в преобразовании плотности вероятности нормального распределения.

Пусть случайная величина X подчиняется нормальному закону распределения [см. формулу (4.20)]. Введем замену и =lпх. Тогда плотность вероятностей случайной величины X примет следующий вид:

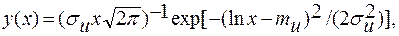(4.71)

где σ_и и т_и уже не имеют того смысла как в исходном уравнении нормального распределения, а связаны с параметрами ряда X следую­щими соотношениями:

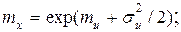(4.72)

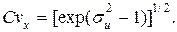(4.73)

Полученное распределение имеет свойства, существенно отличающиеся от исходного нормального распределения. Так, измене­ние случайной величины X ограничено положительной областью. Коэффициент асимметрии связан с коэффициентом изменчивости C_v соотношением

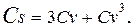(4.74)

Таким образом, логарифмически нормальное распределение по формуле (4.71) более асимметрично, чем распределение Пирсона III типа при C_s = 2C_V.

Вид дифференциальных и интегральных кривых логарифмиче­ски нормального закона распределения представлен на рис. 4.4. Очевидно, что

кривая распределения одномодальна, мода распре­деления находится в точке

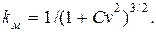(4.75)

При увеличении C_v мода приближается к начальной точке х = 0 и C_s возрастает. Логарифмически нормальным распределе­нием хорошо аппрок-

симируются эмпирические распределения случайных величин, представляющих собой произведения боль­шого числа независимых или слабо зависимых неотрицательных величин, из которых ни одна не является преобладающей.

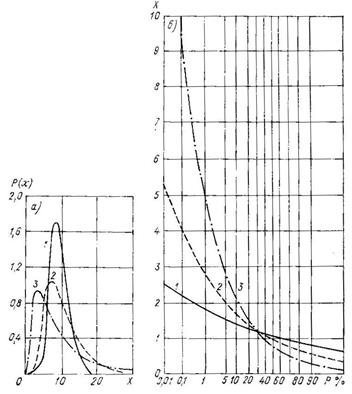
Рис.4.4. Влияние С_v на форму кривой распределения (а) и кривой обеспеченности (б) логарифмически нормального закона распределения.

1 – C_v = 0,25, 2 – C_v = 0,50, 3 – C_v = 1,0