Биномиальное распределение

Пусть производится n испытаний, причём вероятность появления события A в каждом испытании равна p и не зависит от исхода других испытаний (независимые испытания). Так как вероятность наступления события A в одном испытании равна p, то вероятность его ненаступления равна q=1-p.

Пусть событие A наступило в n испытаниях m раз. Это сложное событие можно записать в виде произведения:

.

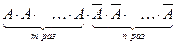Тогда вероятность того, что при n испытаниях событие A наступит m раз 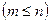, вычисляется по формуле:

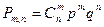
или

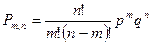(1)

Формула (1) называется формулой Бернулли.

Пример. Пусть всхожесть семян данного растения составляет 90%. Найти вероятность того, что из четырёх посеянных семян взойдут: 1) три; 2) не менее трёх.

1) m=3, n=4, p=0,9, q=1-0,9=0,1,

;

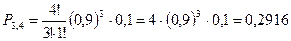2) , ;

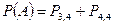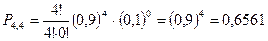P (A) =0,2916+0,6561=0,9477.

Пусть X – случайная величина, равная числу появлений события A в n испытаниях, которая принимает значения 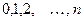с вероятностями:

.

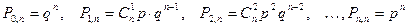Полученный закон распределения случайной величины называется законом биномиального распределения.

X		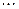		m		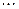n
P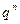

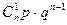
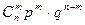
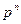
Математическое ожидание, дисперсия и среднее квадратическое отклонение случайных величин, распределённых по биномиальному закону, определяются по формулам:

, , .

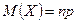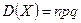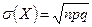Пример. По мишени производятся три выстрела, причём вероятность попадания при каждом выстреле равна 0,8. Рассматривается случайная величина X – число попаданий в мишень. Найти её закон распределения, математическое ожидание, дисперсию и среднее квадратическое отклонение.

p=0,8, q=0,2, n=3, , , .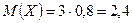

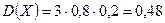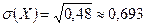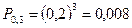- вероятность 0 попаданий;

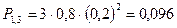- вероятность одного попадания;

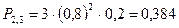- вероятность двух попаданий;

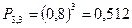- вероятность трёх попаданий.

Получаем закон распределения: