Уравнение кривой распределения
Вернемся к анализу дифференциального уравнения Пирсона (4.3) для кривых плотности распределения вероятности центрированных случайных величин, представленных в модульных коэффициентах. Для определения коэффициентов bi в знаменателе правой части уравнения (4.3) была выведена система уравнений (4.11).
Пусть теперь случайная величина X является заведомо положительной, т.е. хмин ≥0, и положительно асимметричной. Заметим сразу, что положительная асимметричность распределения является характерным свойством многих геоэкологических рядов наблюдений. Так, например, значения концентрации растворенных веществ, стока воды и осадков, как правило, больше или равны нулю, и, следовательно, имеют положительную асимметрию.
Как показано ранее (см. рис. 4.1),
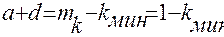 (4.28)
(4.28)
Так как по условию kмин ≥0, то естественно, что a+d ≤ 1. Предположим, что b2 = bз = ... = 0, тогда из системы (4.11) следует
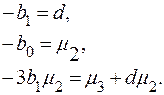 (4.29)
(4.29)
Исходя из этих соотношений можно получить выражение радиуса асимметрии d через второй и третий моменты распределения. Действительно, заменив в третьем уравнении системы (4.27) b1 на - d, получим
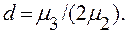 (4.30)
(4.30)
Теперь предположим, что в уравнении (4.3) b2=bз = . . = 0, тогда, предварительно разделив переменные, получим
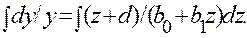
Затем, преобразуем подынтегральное выражение в правой части равенства, умножая числитель и знаменатель на b1 и прибавляя и отнимая в числителе bo. Тогда
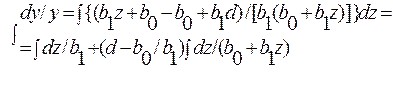
и, решая интегралы в левой и правой частях, уравнения, получаем
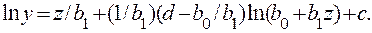 (4.31)
(4.31)
Отсюда
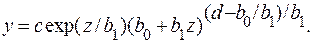 (4.32)
(4.32)
Заметим теперь, что в левой крайней точке распределения, т. е. при минимальном значении z, у = 0. Тогда из уравнения (4.32) при z = zмин получим bo+b1zмин=O, т.е. при b1≠0 для асимметричного распределения zмин = - bo/b1.
Так как расстояние от zмин до центра распределения тк равно (a+d) (см. рис. 4.1), то можно записать
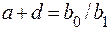
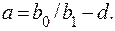 (4.33)
(4.33)
Используя соотношение (4.33) и определяя b1 по системе (4.29), получаем
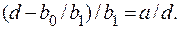 (4.34)
(4.34)
Перенесем начало отсчетов по оси абсцисс в точку, соответствующую моде распределения. Тогда отсчеты относительно моды в случае положительной асимметрии 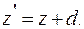
Преобразуем множитель уравнения (4.32), стоящий в скобках, заменив значения z на z' и подставив значение а по формуле (4.33).Тогда
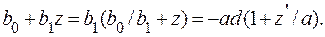 (4.35)
(4.35)
Подставим выражения (4.34) и (4.35) в исходное уравнение (4.32)
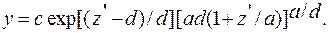 (4.36)
(4.36)
Дальше для удобства будем обозначать z' через z, имея в виду, что z теперь — отсчет по оси абсцисс от моды. Преобразуем полученное выражение, сгруппировав отдельно все параметры, не зависящие от z, и обозначив их через С. Тогда
y= C exp(-z/d)(1+z/a)a/d (4.37)
При z = 0, т. е. в моде распределения значение у (плотность вероятности) будет максимальным. Обозначим это значение через уо. Из уравнения (4.35) получаем для z= 0, уо=с. Тогда окончательный вид уравнения кривой Пирсона III типа при отсчете z относительно моды распределения
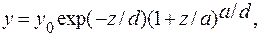 (4.38)
(4.38)
где уо — максимальная ордината распределения.
Выразим теперь параметры a и d через Cv и Cs. При этом, согласно формулам (3.32), (3.33) в данном случае,
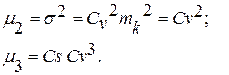
Подставим эти выражения моментов в формулу (4.28). Тогда радиус асимметрии
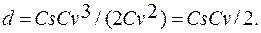 (4.39)
(4.39)
После подстановки в формулу (4.33) значений bo и b1 из системы (4.27) получим
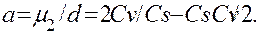 (4.40)
(4.40)
Из формул (4.33) и (4.40) следует, что расстояние от центра распределения до его левого конца
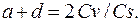 (4.41)
(4.41)
В соответствии с формулой (4.26) a+d=1-кмин Отсюда получаем выражение, связывающее коэффициент асимметрии с величиной кмин,
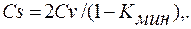 (4.42)
(4.42)
Из формулы (4.42) следует, что Cs ≥2 Cv, а если kмин=0, то Cs =2 Cv.
Таким образомзначения Cs для кривой Пирсона III типа всегда больше или равны 2CV.
4.4.2. Запись уравнения кривой распределения Пирсона III типа через гамма-функцию
Вернемся к уравнению кривой Пирсона III типа относительно центра тяжести (4.30) и перенесем начало отсчета по оси абсцисс в точку zмин где плотность вероятности у = 0. Тогда расстояние по оси абсцисс в новой системе координат будет следующим:
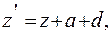 (4.43)
(4.43)
где z — отсчет от центра распределения тk = 1.
С учетом формул (4.34) и (4.43) получим для значения суммы в скобках формулы (4.35) следующие выражения:
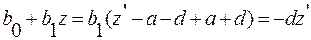 (4.44)
(4.44)
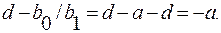 (4.45)
(4.45)
Подставляя эти значения в формулу (4.34), получаем
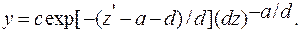 (4.46)
(4.46)
Сгруппируем параметры, не зависящие от z, и обозначим их через сводный параметр с, а z’ – через z, тогда
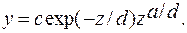 (4.47)
(4.47)
Выразим теперь значения d и a через Cs и Cv [см. формулы (4.39) и (4.40)]
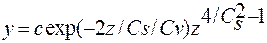 (4.48)
(4.48)
и обозначим
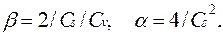 (4.49)
(4.49)
Тогда
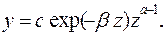 (4.50)
(4.50)
Можно показать, что
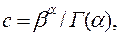 (4.51)
(4.51)
где Г(α) – гамма-функция [16].
После подстановки значения с в уравнение (4.50) получаем уравнение биномиальной кривой распределения или кривой Пирсона IIIтипа для условия Cs = 2CV в отсчетах z от нуля графика (Кмин = 0). С достаточной точностью, так как возможное Кмин для многих рядов стока достаточно близко к нулю, это уравнение можно использовать и для случая, когда Cs > 2CV
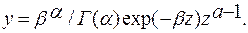 (4.52)
(4.52)
Запись кривой Пирсона IIIтипа через гамма-функцию нередко называют трехпараметричсским гамма-распределением. При использовании его следует учитывать, что X задается в модульных коэффициентах.
Если принять, что Cs = 2Cv то из формул (4.37), (4.38) получаем
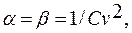 (4.53)
(4.53)
и тогда
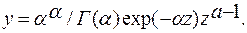 (4.54)
(4.54)
Полученное для частного случая CS = 2CV распределение называется гамма-распределением. В этом случае zi = ki.
Дата добавления: 2020-10-25; просмотров: 662;











