Уравнение кривой распределения

<3 4 567 8 9 >

Семейство кривых трехпараметрического гамма-распределения предназначенных для расчета статистических рядов, значения которых

изменяются от 0 до ∞, было предложено в 1946 г. С. Н. Крицким и М. Ф. Менкелем. Оно основано на модификации уравнения кривой Пирсона III типа при C_S = 2C_V. Подобное изложение этого распределения приводится в монографиях [9, 30].

Уравнение кривой Пирсона III типа при C_S = 2C_V является двухпараметрическим, так как зависит только от двух аргументов m_x и C_v. Положительным качеством гамма-функции является то, что значение X изменяется, как и требуется по условию задачи, от 0 до ∞, т.е. не имеет отрицательных значений, что в большей степени соответствует природе речного стока. Однако соотношение C_S = 2C_V является только одним из частных случаев возможных распределений природных процессов. Поэтому для того, чтобы сделать уравнение (4.53) более общим, С. Н. Крицкий и М. Ф. Менкель прибегли к трансформации исходного признака распределения z. С этой целью в уравнение (4.52) вместо z было введено и, т. е.

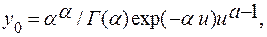(4.57)

где u связано с z соотношением

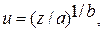(4.58)

где а и b — параметры, которые являются функциями C_v и C_s и подлежат определению на основании данных наблюдений.

Пусть плотность кривой распределения и задана выражением (4.57). Найдем плотность вероятностей распределения z.

Как известно, плотность распределения монотонно возрастающей функции одного случайного аргумента записывается в виде

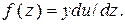(4.59)

Так как функция z = f(u) является монотонно возрастающей, то уравнение кривой распределения z после подстановки значения du/dz по формуле (4.58),

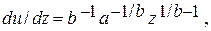(4.60)

может быть представлено в виде

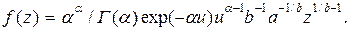(4.61)

Если выразить значения и через z и учесть, что при C_S = 2C_V z_i = K_i, то

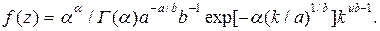(4.62)

Координаты кривой обеспеченности трехпараметрического закона распределения задаются в виде ряда таблиц (см., например, работу [63], прилож. 5), составленных Д. В. Коренистовым, Е. Г. Блохиновым и Н. В. Никольской для определенного соотношения j = C_S/C_v (j = 0,5; 1,0; 1,5; 2,0; 2,5; 3,0; 3,5; 4,0; 5,0; 6,0). В каждой таблице приводятся для данного значения j координаты кривой обеспеченности в модульных коэффициентах: k_P = f(P, C_v), для C_v, изменяющегося от 0,1 до 2,0 с интервалом ΔСv = 0,1.

4.5.2. Свойства распределения

Рассматриваемое распределение определяют три параметра: математическое ожидание т_х, коэффициент вариации C_v и коэффициент асимметрии С_s., причем C_s может принимать как положительные, так и отрицательные значения. При всех сочетаниях C_s (C_s>0) и С_v изменение исследуемой величины ограничено интервалом 0 ≤ х <∞. Вид кривых распределения зависит от соотношения между параметрами а и b. При а > b для b > 0 и произвольном (положительном) значении а для b < 0 мода распределения находится в точке

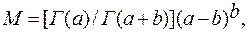(4.63)

а малым значениям X соответствуют малые значения плотности вероятности. При а ≤b и b > 0 мода распределения совпадает с началом кривой, т. е. М = 0.

При C_S = 2C_V и a = b=1 кривые обеспеченности Крицкого-Менкеля совпадают с аналогичными кривыми гамма-распределения.

Основное преимущество кривых обеспеченности Крицкого— Менкеля заключается в том, что при любых соотношениях между C_s и C_v (C_s > 0) нижний предел варьирующего признака равен нулю. Важным обстоятельством является также то, что, в отличие от кривых Пирсона III типа, в данном случае значение C_s не связано с началом кривых.

На рис. 4.3 представлены кривые обеспеченности Крицкого— Менкеля при различных значениях C_s и C_v.

Примеры расчета кривых обеспеченности Крицкого—Менкеля приведены в работах [9,30].

<3 4 567 8 9 >

Дата добавления: 2020-10-25; просмотров: 455;