Дифференциальное уравнение кривых плотности вероятности пирсона

На рис. 4.1. представлен общий вид графика плотности вероятностей случайной величины X, относительно которой известно, что она подчиняется одномодальному закону распределения и ее коэффициент асимметрии C_s ≥ 0. По оси абсцисс здесь отложены значения X в модульных коэффициентах k_i = x_i/m_x.. По оси ординат отложена плотность распределения f(k). В дальнейшем при выводах для упрощения записей будем обозначать f(k) через y. Расстояние по оси абсцисс от математического ожидания до моды - радиус асимметрии — обозначим через d; расстояние от моды до минимального значения — через а.

Отметим основные свойства представленного графика плотности распределения вероятностей.

1. Значения случайной величины X заключаются в определенных пределах. Плотность распределения, соответствующая значениям меньше наименьшего и больше наибольшего предела, равна нулю. (Меньше нуля плотность быть не может, так как она всегда заведомо положительна. См. разд. 3.1.3)

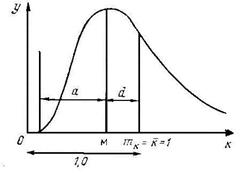
Рис. 4.1 График плотности распределения случайной величины (х≥0) в модульных коэффициентах (k_i=x_i/m_x).

2. Так как в данном случае распределение одномодальное, то в промежутке между наибольшим и наименьшим значениями X плотность вероятности сначала возрастает, начиная от нуля до некоторого максимального значения, а затем снова убывает до нуля.

3. Полная площадь, ограниченная кривой распределения и осью абсцисс (см. разд. 3.1.3), равна 1.

4. Математическое ожидание случайной величины K равно еди­нице, то есть m _k =1

Таким образом, график плотности распределения вероятностей y = f(k) должен удовлетворять следующим условиям: во-первых, в начале и в конце графика по оси абсцисс у = 0; во-вто­рых, где-то между началом и концом графика значение у должно достигать максимума. Таким образом, скорость изменения функции y = f(k), или выражающая эту скорость первая производная dy/dx, должна равняться нулю в трех точках: в начале и в конце распределения, где у=0, и в моде, где плотность распределения достигает максимума.

Для дальнейшего описания графика плотности вероятностей перенесем начало отсчета по оси k в центр распределения, то есть центрируем последовательность значений k. Очевидно, это аналогично тому, что из каждого отсчета к_i, вычитается т_k, равное (см. выше) 1. Обозначим отсчеты по оси абсцисс относительно т_k через z, т. е. z_i = к_i -1.

На основе изложенных свойств Пирсон представил дифференциальное уравнение кривых плотности вероятности центрированных случайных величин в модульных коэффициентах в следующем виде:

dy/dz=y(z+d)/F(z) (4.1)

где F(z) —функция переменной величины z.

Это уравнение действительно соответствует изложенным выше условиям, так как на концах распределения у = 0 и следовательно dy/dz = 0, а при z = -d, т. е. в точке максимума, dy/dz также равно нулю.

Для расчета значений у по z необходимо определить F(z).Для этого будем рассматривать такие функции F(z), которые раскладываются в строку Маклорена.

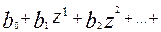
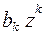
F(z) = (4.2)

При этом вполне достаточно взять три первых члена разложения. Тогда

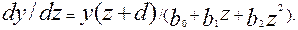(4.3)

Значения z и d в формуле (4.3) предполагаются известными. Необходимо найти значения b₀, b₁, b ₂. Для этого приведем обе части уравнения (4.3) к общему знаменателю и умножим левую и правую части на zⁿ

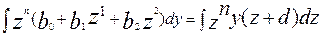(4.4)

Введем следующие обозначения:

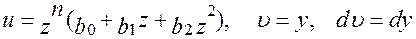
и проинтегрируем левую часть уравнения (4.4) по частям. Получаем:

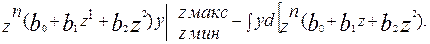(4.5)

Так как на концах распределения у = 0 (см. выше),то первое слагаемое данного выражения равно нулю. Продифференцировав произведение в квадратных скобках, получим выражение для второго слагаемого

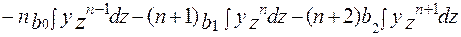(4.6)

Выразим полученные слагаемые через центральные моменты.

Как следует из формулы (3.24), центральные моменты различного порядка могут быть представлены в виде

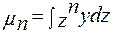(4.7)

где z (см. выше)— центрированная случайная величина, у— плотность распределения.

Подставляя эти значения в формулу (4.6), получаем решение интеграла в левой части уравнения (4.4)

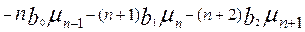(4.8)

Проинтегрируем теперь правую часть уравнения (4.4), подставив значения моментов по формуле (4.7):

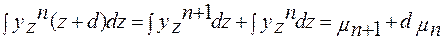(4.9)

Объединим преобразованные правую (4.9) и левую (4.8) части уравнения (4.4)

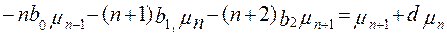(4.10)

и рассмотрим полученное уравнение при значениях п, равных 0, 1, 2.

Так, при п = 0

,

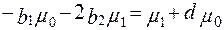при n=1

,

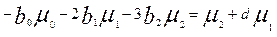при n=2

.

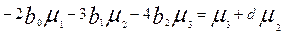Учитывая, что μ₀=1, μ₁= 0 (см. раздел 3.1.4), получаем для определения параметров b_o, b₁, b₂ систему из трех уравнений

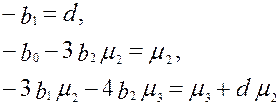(4.11)

Очевидно, что учет других значений b практически излишен, так как даже для расчета b₂, как следует из полученной системы, уже требуется знать 4 момента: μ_0, μ_1, μ_2, μ_3. В то же время точность расчета уравнений в значительной степени понижается с увеличением порядка μ.

В зависимости от значений коэффициентов bo, b₁, b₂ можно по­лучить различные типы кривых обеспеченностей Пирсона. Из них очень широкое распространение получил III тип кривых Пирсона. Поэтому детальный анализ его с выводом основных расчетных формул дается ниже. Кроме того, из дифференциального уравнения кривых Пирсона легко вывести нормальный закон распределения, имеющий самостоятельное значение в геоэкологии.