Ансамбль Гиббса. Уравнение Лиувилля.

Предположим, что мы наблюдаем за системой в течение достаточно длительного времени. Разделим это время на большое количество одинаковых интервалов, разделённых интервалами t₁, t₂… В эти моменты фазовая точка будет находиться в (q_1,p₁); (q_2,p₂) и т.д. Совокупность этих точек будет распределена в фазовом пространстве с плотностью ρ(q,p) – собственно по смыслу функции ρ. Приём Гиббса состоит в следующем: вместо того, чтобы следить за одной системой в течение длительного времени, ввести в рассмотрение большое количество одинаковых (одинаково устроенных) систем, находящихся при t=0 в состояниях (q_1,p₁); (q_2,p₂) … и т.д. Этот набор и представляет собой статистический ансамбль Гиббса. Передвижение фазовых точек этих систем во времени будет происходить согласно уравнениям механики. Ясно, что в каждый момент времени t с тем же правом, что при t=0, эти точки распределены фазовом пространстве согласно той же функции распределения ρ(q,p).

Другой подход: если проводится макроскопический опыт, то мы, естественно, не знаем все q_i,p_i в t=0, так как условия опыта этого не определяют. Мы этого не знаем, знаем только начальные условия для макроскопических величин. q и p могут быть различны при этом, и, следовательно – различные фазовые траектории. Для q и p – только функция распределения. Но в статистическом смысле – это и есть одинаковые макроскопические системы – ансамбль Гиббса.

Эволюция функции распределения ρ(q,p) происходит в результате изменения со временем положения точек {q_i,p_i}, характеризующих состояние системы – ансамбля Гиббса в различные моменты. Это изменение можно представить как течение «жидкости» или «газа» в 6N-мерном пространстве. Поскольку полное число систем ансамбля предполагается заданным (нет источников и стоков), то функция ρ(q,p) подчиняется соответствующему уравнению непрерывности.

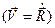(9)

Естественно и div здесь 6N-мерный вектор. div в 6N-мерном пространстве (6N=2f):

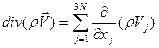
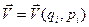
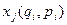- совокупность

или, поскольку мы условились, что движение частиц подчиняется законам механики (1), то

=divV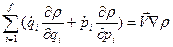

Первый член в правой части равен 0

Имеем:

=0 – уравнение Лиувилля (10)

Учтём, что:

- классическая скобка Пуассона

Другая запись (10):

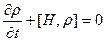
Итак, имеем: →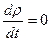

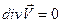1)фазовая жидкость несжимаема

2)вдоль фазовой траектории функция распределения сохраняется (теорема Лиувилля)

И то, и другое – следствия (1) – уравнений механики!!!

А когда ими, собственно, можно ограничиться (пользоваться)? Только если система замкнута – нет взаимодействия с другими. Реально этого нет, можно говорить о квазизамкнутых системах (подсистемах), где энергия взаимодействия (Н_вз) мала по сравнению с собственной энергией (Е).

Пусть R – размер системы

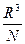- объём на дну частицу ( 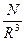- плотность)

- расстояние между частицами

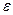( - энергия одной частицы) – энергия в системе объёмом V (V~R³)

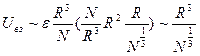
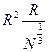- объём поверхности, где взаимодействие

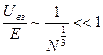, так как N>>1

Таким образом, речь идёт о детерминированном движении, а статически описываются только начальные условия.