Назначение теоретических законов распределения

При проектировании, строительстве и эксплуатации хо­зяйственных систем, а также при решении ряда научных задач необходимо произвести оценку различных характеристик состояния окружающей среды и ее возможных естественных и антропогенных изменений. Для потребителей этой информации было бы желательно, чтобы такая информация представляла собой абсолютно точное значение, например, величины и времени прохождения экстремальных значений стока на весь пе­риод работы каждой конкретной водохозяйственной установки. Однако, как отмечалось выше(см.гл.2), такие однозначные прогнозы в принципе невозможны вследствие вероятностной природы геоэкологических процессов. В тоже время наблюденные экстремальные значения потребителя часто не удовлетворяют потребителя информации. Дело в том, что с увеличением периода наблюдений максимальные значения рассматриваемых характеристик могут увеличиваться, а минимальные уменьшаться, т.е. и максимальные и минимальные значения есть соответственно неубывающие и невозрастающие функции продолжительности периода наблюдений. Поэтому проблема определения возможных значений характеристик изучаемых процессов ре­шается на основе использования теории вероятностей.

Обычно в геоэкологических исследованиях наибольшее внимание уделяется анализу средних значений показателей экологического состояния окружающей среды. При этом, не учитываются, или учитываются в недостаточной степени, возможные отклонения действительных значений показателей от их средних значений. Между тем именно эти отклонения нередко определяют возможные экстремальные значения, вызванные неблагоприятным сочетанием различного рода антропогенных и естественных факторов, и представляют часто не меньший, а может быть и больший практический интерес, чем осредненные характеристики. Действительно, например, практическая значимость изменений средних значений характеристик экологического состояния рассматриваемых объектов может и, как правило, проявляется в многолетней перспективе, когда еще есть возможность принятия мер по обеспечению экологической безопасности. В отличие от этого экстремальные значения характеристик экологического состояния, связанные с загрязнением природной среды, чаще всего проявляются немедленно и нередко сказываются в изменении общей экологической ситуации, как минимум, на ближайшую перспективу. Именно эти резкие отклонения характеристик экологического состояния от среднего значения часто определяют экологическую безопасность не только в каком-то микрорайоне, но и на больших территориях, включающих целые регионы.

Имеющиеся в настоящее время исследования экстремальных уровней изменений окружающей среды в основном опираются на экологически допустимые уровни нагрузки на экосистемы. При этом в качестве экстремальных принимаются максимальные и минимальные значения показателей качества окружающей среды за период наблюдений, или значения этих показателей обеспеченностью 5 и 95 % [ ]. Между тем, обеспеченность, уже наблюденных значений (см. ниже), нередко выходит за названные пределы, и нет никаких гарантий, что в будущий период не появятся значения показателей загрязненности, превышающие уже наблюденные.

Все это говорит о том, что изучению экстремальных характеристик возможных значений характеристик окружающей среды, причинам их появления и методам их оценок, расчетов и прогнозов должно уделяться в геоэкологии большее внимание, чем это делается в настоящее время.

Задачи, которые встают перед геоэкологами, при оценке экстремальных значений характеристик окружающей среды, весьма разнообразны. Так, для обеспечения потребителей необходимым минимумом речной воды нужно знать, как часто расход воды будет равен или превысит заданный минимум. Если, например, минимальный сток равен или превышает необходимый минимум Q_мин только в 80 % случаев (т. е. обеспеченность Q_мин составляет 80%), то, по-видимому, при проектировании следует предусмотреть другие источники водоснабжения, так как, примерно, 1 раз в пять лет речной воды будет недостаточно. Если обеспеченность Q_минсоставляет 99 %, то можно считать, что, за редким исключением, других источников водоснабжения в данном случае не потребуется.

Другой пример. Для пропусков больших расходов при строи­тельстве и эксплуатации плотин необходимо рассчитать водосбросные отверстия. Теоретически можно предусмотреть такие большие размеры этих отверстий, что они будут всегда, в любой по водности год, достаточны для сброса воды. Но, так как максимально возможные расходы воды и гидрограф стока неизвестны, то в этом случае размер отверстий должен быть очень большим. Однако такое решение задачи практически невозможно из-за их большой стоимости. Поэтому для ее решения используют другой подход, который заключается в том, что в качестве расчетного значения расхода при определении размера отверстий принимается расход Q_P обеспеченностью Р равной 0,01; 0,1; 1,0; 3,0 % и т. д. Причем обеспечен­ность назначается с учетом класса сооружений и тех последствий, которые могут быть при превышении фактического расхода воды над рассчитанным [30].

Можно привести еще множество примеров, когда потребителю информации, в том числе и самим геоэкологам, не­обходимо знать режимные характеристики тех или иных объектов той или иной обеспеченности.

Однако определение обеспеченных значений режимных характеристик часто является сложной, далеко не тривиальной задачи. Дело в том, что, как отмечалось ранее, имеющиеся ряды наблюдений обычно непродолжительны и определение, например, значений заданной обеспеченности непосредственно по эмпирическим данным не дает удовлетворительных результатов. Действительно, по любому ряду X (x₁, x₂, .. ., х_п) могут быть рассчитаны только эмпирические обеспе­ченности (см. разд. 3.3). Как отмечалось выше, лишь при неограниченном увеличении числа членов в выборке, или в данном случае периода наблюдений, эмпирическая обеспеченность 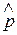, согласно теореме Бернулли [61], сходится по вероятности к действительной обеспечен­ности (вероятность превышения) р.

Таким образом, необходимо, зная эмпирические обеспеченно­сти значений ряда X, определить действительные значения этих обеспеченностей. В исследованиях эта задача по­лучила название: задача сглаживания или задача интерполяции эмпирических кривых обеспеченностей.

Кроме того, если для наблюденных значений ряда х₁, х₂, ..., х_п можно с какой-то степенью точности указать обеспечен­ность их в будущий период, то определить обеспеченность воз­можных значений X, которые в имеющийся период не наблюда­лись, без дополнительной информации вообще невозможно. Так, продолжительность имеющихся рядов годового стока позволяет вычислить значения расхода воды, эмпирическая обеспеченность, которого составляет, за редким исключением, не менее 1 —10%. А для проектирования водохозяйственных сооружений необходимо знать, в зависимости от класса сооружения, расход обеспеченно­стью 0,01, 0,1, 1, 99 % и др. Таким образом, возникает задача экстраполяции кривых обеспеченностей в верхней и нижней части.

В настоящее время эти задачи решаются на основе анализа законов распределения случайной величины.

Из множества известных законов распределения в гидрометеорологии наибольшее распространение получили: дискретные законы распределения: биномиальный и Пуассона; непрерывные законы распределения: нормальный, Пирсона III типа, Крицкого — Менкеля, логарифмически нормальный, Гумбела, Гудрича, Джон­сона.

.