Аналогично преобразуем и уравнение движения
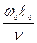 (Wx
(Wx 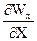 + Wу
+ Wу 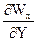 ) =
) = 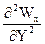 +
+ 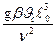 ×
× 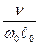 ×Q
×Q
Rе º w0 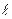 0/n - число Рейнольдса – характеризует соотношение сил инерции и сил вязкости
0/n - число Рейнольдса – характеризует соотношение сил инерции и сил вязкости
Gr º gbuc 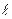 03/n2 - число Грасгофа – характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей
03/n2 - число Грасгофа – характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей
Известно, что коэффициент теплоотдачи при известном температурном поле определяется по уравнению:
a = - 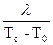 (
( 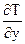 )у=0
)у=0
Приведя к записи в безразмерной форме, получим
Þ a 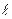 0/l = - (¶Q/¶Y)Y=0
0/l = - (¶Q/¶Y)Y=0
Nu º a 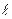 0/l - число Нуссельта или безразмерный коэффициент теплоотдачи – характеризует теплообмен на границе стенка - жидкость
0/l - число Нуссельта или безразмерный коэффициент теплоотдачи – характеризует теплообмен на границе стенка - жидкость
Pr = n/a –число Прандтля Þ мера подобия полей температур и скоростей (а = l/сr)
Þ Ре = Rе ×Pr
при Pr = 1.
Уравнение сплошности в безразмерной форме имеет вид
w0 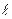 0(¶Wx/¶Х + ¶Wy/¶Y) = 0
0(¶Wx/¶Х + ¶Wy/¶Y) = 0
Граничные условия
1) Y = ¥ Þ Q = Qс = 0; Wx = 1; Wy = 0
2) Y = 0 Þ Q = Qс = 1; Wx = Wy = 0
Таким образом, мы получили систему безразмерных дифференциальных уравнений и безразмерных условий однозначности.
В итоге имеем: Х и Y – независимые переменные; Nu, Q, Wx, Wy – зависимые переменные; Ре, Rе, Gr – постоянные величины.
В результате можно записать уравнения подобия:
Nu = f1(Хc,Yc, Ре, Rе, Gr);
Q = f2(Хc,Yc, Ре, Rе, Gr);
Wx = f3(Хc,Yc, Ре, Rе, Gr);
Wy = f4(Хc,Yc, Ре, Rе, Gr);
Критерии подобия – это числа подобия, составленные из наперед заданных параметров (постоянных) математического описания процесса.
Дата добавления: 2021-09-07; просмотров: 795;











