А плотность распределения вероятности промежутков времени между заявками

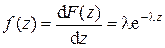. (2.10)

Таким образом, распределение промежутков времени между заявками простейшего потока подчиняется показательному (отрицательному экспоненциальному) закону. Функция F(z) зависит от параметра потока l.

Характеристики промежутков времени между заявками Z можно записать в виде

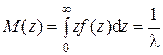, (2.11)

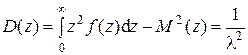, (2.12)

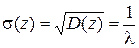. (2.13)

Из (2.11) и (2.13) следует, что M(z) = s(z). Такое равенство характерно для показательного закона распределения любой случайной величины. Формула (2.11) показывает, что с увеличением параметра потока l уменьшается математическое ожидание промежутка времени между заявками M(z).

Распределение промежутков времени между заявками по показательному закону (2.9) является не только необходимым, но и достаточным условием существования простейшего потока. Можно показать, что поток с независимыми промежутками между заявками, распределенными по одинаковому показательному закону (2.9), является простейшим потоком.

Показательный закон обладает следующим свойством: если промежуток времени, распределенный по показательному закону, уже длится некоторое время, то это никак не влияет на закон распределения оставшейся части промежутка; он будет таким же, как и закон распределения всего промежутка. Для доказательства предположим, что промежуток времени между заявками равен t. Найдем по условию вероятность того, что он будет продолжаться еще не менее времени t. На основании теоремы умножения вероятностей можно записать

P(z > t + t) = P(z > t) P(z > t/z > t).

С учетом (2.9)

e^–l(t+t) = e^–lt P(z > t/z > t),