Амплитуда рассеянной волны решеткой точечных атомов. Уравнение дифракции Лауэ
Если необходимо знать интенсивность излучения, рассеянного пространственным распределением электронов внутри каждой элементарной ячейки, то необходим более подробный анализ. Наиболее простой метод предложен Лауэ, который состоит в суммировании вкладов от элементарных волн, рассеянных от каждого элемента кристалла.
Найдем направления распространения волн, выходящих из кристалла, относительно заданного направления распространения падающей волны и рассчитаем интенсивность дифракции электромагнитного излучения (фотонов) на кристаллической решетке, имеющей примитивную элементарную ячейку в виде косоугольного параллелепипеда с векторами 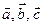 . Пусть вдоль векторов
. Пусть вдоль векторов 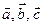 решетка имеет соответственно по N, M, P узлов (см. рис. 2.2).
решетка имеет соответственно по N, M, P узлов (см. рис. 2.2).
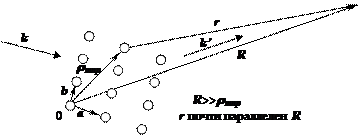
|
| Рис. 2.2. Рассеяние электромагнитных волн узлами кристаллической решетки. |
Пусть на такую решетку падает волна с волновым вектором 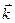 , и частотой
, и частотой 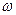 , а отраженная волна имеет волновой вектор
, а отраженная волна имеет волновой вектор 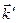 и частоту
и частоту 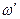 . Рассмотрим случай, когда не происходит изменения частоты у рассеянного излучения:
. Рассмотрим случай, когда не происходит изменения частоты у рассеянного излучения: 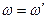 , а значит (так как
, а значит (так как 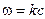 ) и
) и 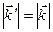 .
.
Выразим направление отраженной волны через волновой вектор падающей волны 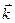 и векторы примитивных трансляций
и векторы примитивных трансляций 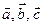 кристаллической решетки.
кристаллической решетки.
Вектор напряженности электрического поля 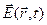 в падающей волне в точке
в падающей волне в точке 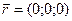 пусть задается как
пусть задается как
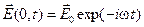
Вектор напряженности электрического поля 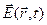 в падающей волне в точке
в падающей волне в точке 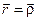 пусть задается как
пусть задается как
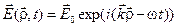
Вектор напряженности электрического поля 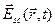 в рассеянной волне в точке
в рассеянной волне в точке 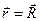 :
:
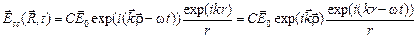 (25)
(25)
С- коэффициент пропорциональности
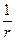 - для сохранения энергии в потоке рассеянной волны.
- для сохранения энергии в потоке рассеянной волны.
Эта волна взаимодействует с рассеивающим центром, находящимся в точке ρ, в результате чего образуется рассеянная волна, выражение для которой можно записать в виде:
Наша задача заключается в суммировании элементарных волн, рассеянных всеми центрами рассеяния в кристалле, в результате чего мы получим амплитуду суммарной рассеянной волны в точке с радиус-вектором R, проведенным из начала координат О внутри кристалла. В этой точке расположен счетчик фотонов. Из рис.2.15 мы видим, что расстояние между рассеивающим центром и точкой наблюдения равно.
Для вектора 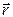 можно записать (см. рис.2.2.):
можно записать (см. рис.2.2.):
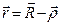
Возведя обе части выражения в квадрат, получим:
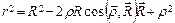
Если извлечь квадратный корень и пренебречь членами порядка 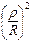 и выше, то получим:
и выше, то получим: 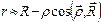 .
.
Тогда полный пространственный фазовый множитель рассеянной волны в выражении (25) можно представить в виде:
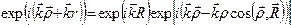
Так как 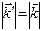 , а направление вектора рассеянной волны
, а направление вектора рассеянной волны 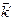 совпадает с направлением
совпадает с направлением 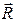 , то
, то
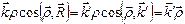
Следовательно, фазовый множитель можно записать так:
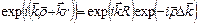
где 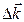 - изменение волнового вектора в результате рассеяния:
- изменение волнового вектора в результате рассеяния: 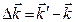
с учетом вышеизложенного волну, рассеянную центром рассеяния в точке 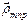 , можно представить как :
, можно представить как :
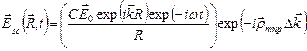
Выражение для суммарного рассеяния в данном направлении от решетки точеных атомов можно получить с помощью суммирования выражения (33) для 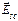 по всем точкам решетки. В этом случае сумма фазовых множителей определяется как:
по всем точкам решетки. В этом случае сумма фазовых множителей определяется как:
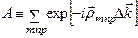
Кристалл имеет форму параллелепипеда и каждый узел решетки рассеивает падающую волну. Центры рассеяния расположены в каждом узле этой решетки: 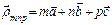 , где m,n,p – целые числа. Тогда величина суммарного рассеянного излучения пропорциональна
, где m,n,p – целые числа. Тогда величина суммарного рассеянного излучения пропорциональна
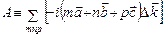
Величину А называют амплитудой рассеяния.
Сумма, взятая по узлам решетки, максимальна, когда 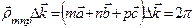 (*)
(*)
для всех узлов решетки, так как каждый член, имеющий форму 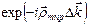 , равен единице.
, равен единице.
Величина 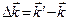 удовлетворяет условию дифракции (*), если одновременно выполняются соотношения для целых чисел h,k,l:
удовлетворяет условию дифракции (*), если одновременно выполняются соотношения для целых чисел h,k,l:
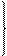
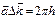
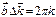 уравнение дифракции Лауэ
уравнение дифракции Лауэ
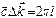
Рассмотрим вектор 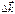 , равный
, равный 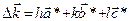 ( ),
( ),
где h,k,l – целые числа, входящие в уравнение Лауэ ( ).
Подставляя 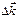 из ( ), видно, что ( ) есть решение уравнений ( ), если
из ( ), видно, что ( ) есть решение уравнений ( ), если
1. 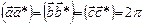
2. 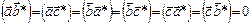
Следовательно, 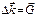 , где
, где 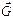 - вектор обратной решетки (смотри лекцию №1).
- вектор обратной решетки (смотри лекцию №1).
Таким образом, условие дифракции: 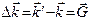
Возведем обе части этого соотношения в квадрат и получим:
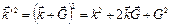
Так как 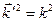 , то
, то 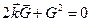 (**)
(**)
Соотношение (**) эквивалентно закону Брэгга-Вульфа.
2.3. Геометрическая интерпретация уравнения Лауэ. Построение Эвальда.
Пространство обратной решетки называется пространство Фурье. В Фурье пространстве правило отбора 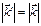 и
и 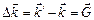 имеют геометрическую интерпретацию – построение Эвальда (рис. 2.3).
имеют геометрическую интерпретацию – построение Эвальда (рис. 2.3).
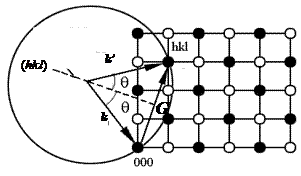
| ||
| Рис. 2.3. Построение Эвальда. |
Построение Эвальда заключается в следующем:
1. Найдем обратную решетку кристалла, подсчитав длины 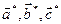 . Построим сетку обратной решетки. Выберем узел обратной решетки за начальный. Направление вектора
. Построим сетку обратной решетки. Выберем узел обратной решетки за начальный. Направление вектора 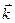 совпадает с направлением падающей волны. Вектор
совпадает с направлением падающей волны. Вектор 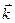 заканчивается на произвольном узле обратной решетки. Обозначим этот узел 0 0 0.
заканчивается на произвольном узле обратной решетки. Обозначим этот узел 0 0 0.
2. Рисуем сферу радиусом 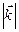 =2p/l с центром в начале вектора
=2p/l с центром в начале вектора 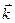 . Если сфера пересекает еще один узел обратной решетки – наблюдается дифракция. Дифрагированная волна распространяется вдоль
. Если сфера пересекает еще один узел обратной решетки – наблюдается дифракция. Дифрагированная волна распространяется вдоль 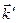 .
. 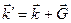
Построением Эвальда очень удобно пользоваться для предсказания углов поворота кристалла и направления дифрагированных лучей. Обратная решетка жестко связана с кристаллической решеткой кристалла, при повороте кристалла вместе с ним поворачивается и обратная решетка. Для наблюдения дифракции кристалл поворачивают так, чтобы вектор рассеяния совпал бы с одним из узлов обратной решетки. С помощью геометрии можно вычислить необходимые углы поворота обратной решетки (и кристалла), а затем определить, под какими углами должен быть расположен детектор излучения, регистрирующий волны с вектором 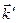 .
.
Из рис. 2.3 видно, что между длинами векторов 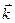 и
и 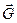 существует связь:
существует связь:
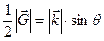 Þ
Þ 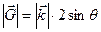 .
.
Так как 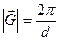 (смотри лекцию №1) и
(смотри лекцию №1) и 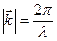 , то
, то
получаем формулу Брэгга-Вульфа: 2dsinq= nl (в данном случае n=1).
Зоны Бриллюэна.
Зона Бриллюэна представляет собой ячейку Вигнера-Зейтца в обратной решетке. Она обладает важным свойством: волны и частицы, волновой вектор которых находится на ее границе, удовлетворяют условию дифракции.
Запишем условие дифракции 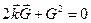 (**) в виде
(**) в виде
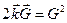 (для удобства
(для удобства 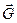 заменили на -
заменили на - 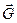 ).
).
Перепишем это выражение в виде:
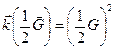
Построим плоскость, перпендикулярную к вектору 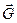 и проходящую через его середину. Тогда произвольный вектор
и проходящую через его середину. Тогда произвольный вектор 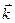 , проведенный до этой плоскости из точки, выбранной из начала координат, будет удовлетворять условию дифракции (рис.2.4). Построенная таким образом плоскость образует часть границы зоны Бриллюэна.
, проведенный до этой плоскости из точки, выбранной из начала координат, будет удовлетворять условию дифракции (рис.2.4). Построенная таким образом плоскость образует часть границы зоны Бриллюэна.
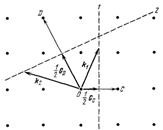
| Рис.2.4. Узлы обратной решетки в окрестности точки О, выбранной за начало координат. Плоскости 1 и 2 являются серединными перпендикулярами к векторам 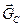 и и 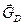 соответственно. Произвольные векторы (например, соответственно. Произвольные векторы (например, 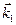 и и 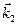 ), проведенные из т. О и оканчивающиеся на плоскостях 1 и 2, удовлетворяют условиям дифракции ), проведенные из т. О и оканчивающиеся на плоскостях 1 и 2, удовлетворяют условиям дифракции
|

|
| Рис.2.5. Квадратная обратная решетка |
Рассмотрим двухмерную квадратную обратную решетку (рис.2.5). Тонкими сплошными линиями показаны векторы обратной решетки 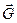 . Пунктирные линии являются серединными перпендикулярами к этим векторам. Квадрат 1, расположенный в центре рисунка, имеет наименьшую площадь из всех квадратов, расположенных в окрестности начала координат. Этот квадрат является примитивной ячейкой Вигнера-Зейтца в обратной решетке. Ячейка Вигнера-Зейтца обратной решетки называется первой зоной Бриллюэна. Симметрия первой зоны Бриллюэнатакая, как у обратной решетки. Зонам Бриллюэна с более высокими порядковыми номерами соответствуют области вне первой зоны Бриллюэна (например, область 2 на рис. 2.5), ограниченные плоскостями, которые проходят через середины отрезков, соединяющих центр первой зоны с остальными узлами обратной решетки, и перпендикулярны этим отрезкам. Вторая зона, третья зона и т.д. состоят из нескольких частей. Объемы всех зон одинаковы.
. Пунктирные линии являются серединными перпендикулярами к этим векторам. Квадрат 1, расположенный в центре рисунка, имеет наименьшую площадь из всех квадратов, расположенных в окрестности начала координат. Этот квадрат является примитивной ячейкой Вигнера-Зейтца в обратной решетке. Ячейка Вигнера-Зейтца обратной решетки называется первой зоной Бриллюэна. Симметрия первой зоны Бриллюэнатакая, как у обратной решетки. Зонам Бриллюэна с более высокими порядковыми номерами соответствуют области вне первой зоны Бриллюэна (например, область 2 на рис. 2.5), ограниченные плоскостями, которые проходят через середины отрезков, соединяющих центр первой зоны с остальными узлами обратной решетки, и перпендикулярны этим отрезкам. Вторая зона, третья зона и т.д. состоят из нескольких частей. Объемы всех зон одинаковы.
Пример: На рис.2.6 представлены одномерные кристаллическая и обратная решетки. Базисным вектором обратной решетки является вектор 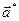 (
( 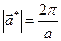 ). Вектор обратной решетки
). Вектор обратной решетки 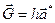 . Кратчайшими векторами обратной решетки, проведенными из начала координат, являются векторы
. Кратчайшими векторами обратной решетки, проведенными из начала координат, являются векторы 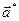 и -
и - 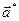 . Серединные перпендикуляры к этим векторам – это и есть границы первой зоны Бриллюэна. На этих границах
. Серединные перпендикуляры к этим векторам – это и есть границы первой зоны Бриллюэна. На этих границах 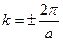 .
.

|
| Рис.2.6. Одномерные кристаллическая и обратная решетки. |
Дата добавления: 2021-05-28; просмотров: 859;











