Формула Гаусса-Лагерра
До сих пор пределы интегрирования были конечные. Но обратите внимание: в квадратурных формулах Гаусса концы отрезка интегрирования не являются узлами квадратурной формулы (в отличие от формул Ньютона-Котеса). Формулы такого типа называются открытыми. Это вселяет надежду, что должны существовать квадратурные формулы для интегралов с бесконечными пределами интегрирования. И они имеются.
На луче xÎ[0,¥) свойством ортогональности с весом r(x)=xs e–x обладают полиномы Лагерра
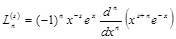 ,
,
где s – любое вещественное число, n – целое положительное число. Следовательно,
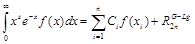 (3.21)
(3.21)
где xi – корни полинома Лагерра n-ой степени. Для них тоже нет общей формулы, поэтому они либо определяются из решения соответствующего алгебраического уравнения, либо из таблиц.
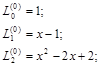
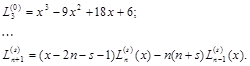
Коэффициенты квадратурной формулы имеют вид:
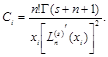
Погрешность квадратурной формулы Гаусса-Лагерра:
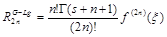 .
.
Здесь Г(x) – гамма–функция. Для целого положительного аргумента k Г(k)=(k–1)!
Например, для s=0 и n=2 формула Гаусса–Лагерра имеет вид

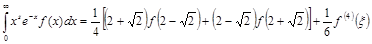 .
.
Дата добавления: 2020-10-25; просмотров: 791;











