Формула прямоугольников

Аппроксимируем подынтегральную функцию полиномом нулевой степени – константой f(x_*), где х_* – единственный узел на отрезке [x_i–1, x_i]. Тогда

.

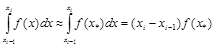В качестве х_* обычно выбирают середину отрезка (известно, что симметрия повышает точность численных формул):

x_* = (x_i–1+x_i)/2=x_i–1/2 .

Таким образом, получаем формулу «центральных» прямоугольников для элементарного отрезка:

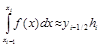, где h_i = x_i–x_i–1; y_i–1/2 = f(x_i–1/2).

Просуммировав, получаем составную (обобщенную) формулу «центральных» прямоугольников:

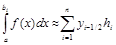. (3.7)

Для равномерной сетки ( h=(b–a)/n ) формула примет вид:

.

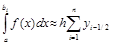В дальнейшем будем рассматривать равномерную сетку.

Теперь оценим погрешность формулы «центральных» прямоугольников.

Сначала попробуем это сделать с помощью погрешности интерполяции (n=0; w(x)=x – x_i–1/2).

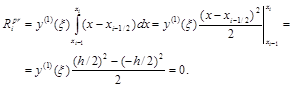
Вывод: формула «центральных» прямоугольников для элементарного отрезка является точной для полиномов степени не только нулевой и первой степени, но и второй.

Оценим погрешность метода с помощью разложения в ряд Тейлора:

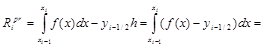
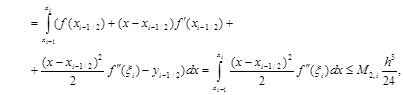где .

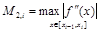Для составной формулы «центральных» прямоугольников

,

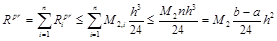где .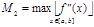

Таким образом, погрешность формулы «центральных» прямоугольников на всем отрезке интегрирования есть величина второго порядка малости по отношению к шагу. Говорят, что квадратурная формула имеет второй порядок точности.

Примечание 3. О формулах «левых» и «правых» прямоугольников.

Можно легко показать (например, с помощью погрешности интерполяции), что при ином выборе узловой точки х_* квадратурные формулы «левых» прямоугольников и «правых» прямоугольников, соответственно

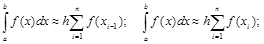
имеют первый порядок точности.

Конец примечания 3.

Формула трапеций

Аппроксимируем подынтегральную функцию полиномом первой степени, построенным по двум узлам: x_i–1 и x_i . Интерполяционный полином Лагранжа первой степени имеет вид

.

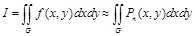Тогда

.

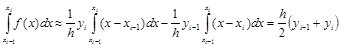Получили формулу трапеций для элементарного отрезка [x_i–1, x_i].

Суммируя, получаем составную формулу трапеций:

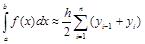. (3.8)

Оценим погрешность формулы трапеции.

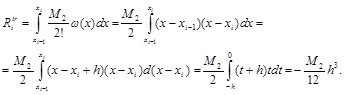
Тогда .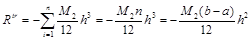

Формула трапеций имеет тот же порядок точности – второй, что и формула центральных прямоугольников, но ее погрешность оценивается величиной в два раза большей. Поэтому предпочтительнее пользоваться формулой прямоугольников.

Примечание 4. О симметричных квадратурных формулах.

Отметим еще один интересный факт. Формула прямоугольников получена при использовании полинома нулевой степени, а формула трапеций – первой. Но порядок точности один и тот же, хотя при увеличении степени полинома следовало бы ожидать увеличения точности. Это проявление симметрии формулы прямоугольников (сравните для примера порядки точности несимметричной формулы левых прямоугольников и формулы трапеций – соответствие степени интерполяционного полинома и порядка точности налицо).

Признаки симметричности квадратурных формул:

1) n – четное;

2) узлы расположены симметрично относительно середины отрезка [a,b], то есть ;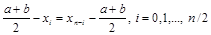

3) коэффициенты симметричны: C_i=C_{n– i} .

Конец примечания 4.

Формула Симпсона

Аппроксимируем подынтегральную функцию полиномом второй степени, построенным по трем узлам: x_i–1, x_i–1/2, x_i . Интерполяционный полином Лагранжа второй степени имеет вид

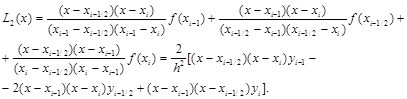
Тогда

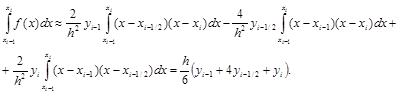
Получили формулу Симпсона для элементарного отрезка [x_i–1,x_i].

Суммируя, получаем составную формулу Симпсона:

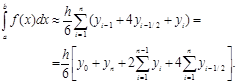(3.9)

Оценим погрешность формулы Симпсона.

Так как эта формула – симметричная, то сразу можно сделать вывод о том, что способ определения погрешности квадратурной формулы по погрешности интерполяционной формулы

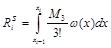
будет безрезультатным (проверьте!). Поэтому используем разложение в ряд Тейлора узловых значений функции в окрестности точки x=x_i–1/2:

.

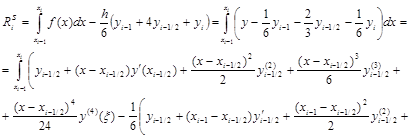
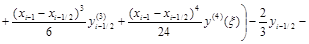
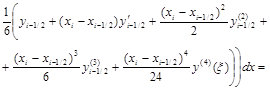
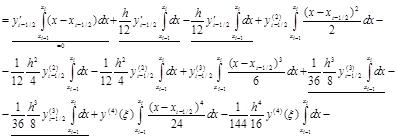
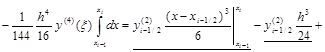
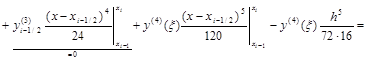
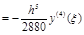Для составной формулы Симпсона

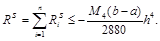
Таким образом, формула Симпсона существенно точнее, чем формула прямоугольников или трапеций. Порядок точности – четвертый.

Примечание 5. О формуле Симпсона без полуцелых точек.

Формулу Симпсона можно записать по-другому, если пронумеровать насквозь и целые, и полуцелые точки.

Тогда n=2m (то есть n – четное число), новый шаг интегрирования h₁ = h/2=(b–a)/(2m), а формула имеет вид:

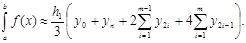(3.10)

Погрешность

.

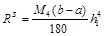Конец примечания 5.