КВАДРАТУРНЫХ ФОРМУЛ
Рассмотрим определенный интеграл
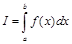 .
.
Если нет возможности выразить интеграл в известных элементарных или специальных функциях, то применяется приближенное численное интегрирование. Кроме того, если подынтегральная функция задана таблично, то значение интеграла также находится численно.
Рассмотрим методы численного интегрирования, основанные на аппроксимации подынтегральной функции интерполяционными полиномами.
Заменяя подынтегральную функцию, например, интерполяционным полиномом Лагранжа, получаем приближенную формулу:
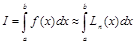 .
.
При этом предполагается, что отрезок [a,b] разбит на n частей точками a = x0 , x1 , ... , xn = b, по которым строят интерполяционный полином.
Подставляя выражение для интерполяционного полинома Лагранжа, получаем
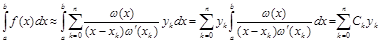 ,
,
где 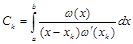 .
.
Таким образом, определенный интеграл можно представить в виде:
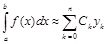 , (3.6)
, (3.6)
причем коэффициенты Ск не зависят от подынтегральной функции f(x), а только от значений узлов интерполяции.
Это приближенное равенство называется квадратурной формулой.[2] Точки хк называются узлами квадратурной формулы, а числа Ск – коэффициентами квадратурной формулы.
Разность
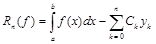
называется погрешностью квадратурной формулы.
Отметим, что: 1) погрешность зависит как от расположения узлов, так и от выбора коэффициентов; 2) если функция f(x) – полином степени n, то тогда квадратурная формула будет точной (то есть Rn(f)º0), так как в этом случае Ln(x)ºf(x); 3) погрешность квадратурной формулы можно также представить в другом виде – как интеграл от погрешности интерполяционной формулы Лагранжа:
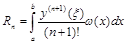 .
.
Получим некоторые простые (и в то же время весьма распространенные) формулы численного дифференцирования, используя интерполяционный полином Лагранжа.
Предварительно отметим, что для получения формул численного дифференцирования на некотором отрезке [a, b] достаточно построить квадратурную формулу для интеграла на элементарном отрезке [xi–1,xi ], а затем ее просуммировать, т.к.
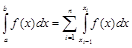 .
.
Дата добавления: 2020-10-25; просмотров: 664;











