Вычисление интегралов от неограниченных функций

Рассмотрим интеграл 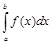от функции, для которой существует точка (точки) сÎ[a;b] такая, что 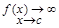(точка разрыва 2-ого рода[7]). Отметим, что эти особые точки можно сразу перевести на границу

.

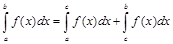Способ 1. Интегрирование по частям.

.

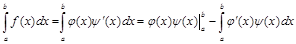Последний интеграл может не иметь особенностей.

Способ 2. Мультипликативное выделение особенности.

,

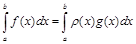где функция r(х) соответствует, например, весовой функции квадратурной формулы Гаусса-Чебышева, а g(x) – ограниченная функция.

Способ 3. Аддитивное выделение особенности.

,

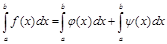где функция j(х) имеет особенность, но легко интегрируется точно (без применения численных методов), а функция y(х) – достаточно гладкая ограниченная функция, чтобы воспользоваться какой-либо стандартной квадратурной формулой.

3.12 ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ КРАТНЫХ

ИНТЕГРАЛОВ. МЕТОД МОНТЕ-КАРЛО

Ограничимся рассмотрением двойных интегралов вида

.

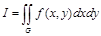Способ 1. Замена подынтегральной функции многомерным интерполяционным полиномом (п.2.9) с последующим простым интегрированием:

.

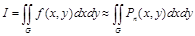Способ 2. Сведение к последовательному вычислению определенных интегралов.

Например, для прямоугольной области интегрирования G (рис.3.2, а))

,

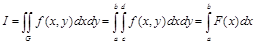где .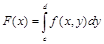

Теперь разбиваем область интегрирования по х на n шагов, а по y на m шагов. Последовательно фиксируем узлы х_i и находим интегралы F(x_i) по какой–либо квадратурной формуле:

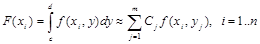
Затем, применяя эту же (или другую) квадратурную формулу, находим искомый интеграл

.

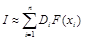Таким образом, 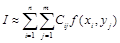, где С_ij=C_j D_i .

Эта формула называется кубатурной формулой. Ее погрешность складывается из погрешностей примененных квадратурных формул и равна .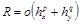

Если же область интегрирования – криволинейная (рис.3.2, б), то ее можно перевести в прямоугольную путем подходящей замены переменных. Например, пусть xÎ [a;b], yÎ[j(x);y(x)]. Тогда замена

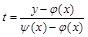
переводит ее в прямоугольную xÎ [a;b], t Î [0;1].

Можно пойти и по другому пути. Строим прямоугольник R ÉG, стороны которого параллельны осям координат (рис. 3.2, в) и рассматриваем вспомогательную функцию

.

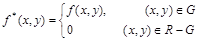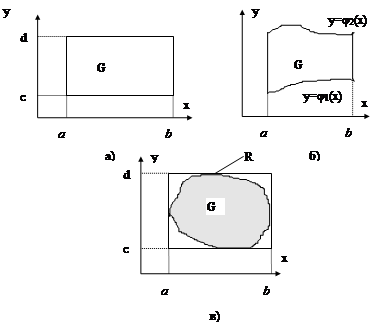Рис.3.2. Двумерные области интегрирования

Тогда, очевидно,

,

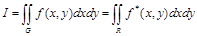и для последнего интеграла строится кубатурная формула.

Способ 3. Метод Монте-Карло.

Особое место среди численных методов занимают вероятностные методы. Все вычислительные алгоритмы, которые рассматривались до сих пор, являлись детерминированными. Это означает, что при любом таком алгоритме результат, соответствующий одному и тому же шагу алгоритма, при многократной реализации алгоритма будет совпадать.

Наряду с детерминированными процессами имеют место процессы заранее непредсказуемые – случайные. Алгоритмы, реализующие случайные процессы, называются вероятностными. Способы решения задач, использующие случайные величины, получили общее название методов Монте-Карло.

В основе оценки искомого значения интеграла I лежит известное соотношение («теорема о среднем»)

,

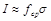где f_cp –значение подынтегральной функции в некоторой «средней» точке области интегрирования, а s – многомерный объем области интегрирования.

Например, для двойного интеграла

,

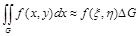где DG – площадь области G.

При этом предполагается, что подынтегральная функция непрерывна в области интегрирования.

Выберем в этой области N случайных точек А_i. При достаточно большом N приближенно можно считать что

.

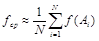Строгое обоснование этой формулы дает закон больших чисел теории вероятности.

Следовательно, приближенная формула для вычисления кратного интеграла I имеет вид:

.

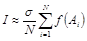Например, для интеграла на отрезке [a,b]

,

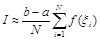для двойного интеграла на прямоугольной области

.

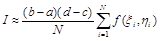Здесь x_i ,h_i – координаты случайных точек, лежащих в заданной области. Эти координаты – случайные числа, то есть значения независимых одинаково распределенных случайных величин.

Таким образом, возникает проблема получения последовательности случайных чисел, лежащих в заданном диапазоне.

В современных ЭВМ случайные числа 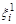, равномерно распределенные на отрезке [0; 1], задаются с помощью специальных программ – датчиков случайных чисел. Строго говоря, они не случайные (раз имеется алгоритм их нахождения!), но практически они обладают статистическими характеристиками, свойственными случайным числам. У каждого алгоритма есть свое число членов последовательности, которое можно использовать в расчетах (период датчика ). При большем числе членов теряется случайный характер чисел, например, может обнаруживаться периодичность. Поэтому, такие числа носят название псевдослучайных.

Чтобы их использовать для получения координат случайных точек A_i , достаточно выполнить преобразование

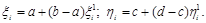
Метод Монте-Карло является универсальным методом вычисления интегралов высокой кратности. Его погрешность 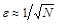, то есть число узловых точек N»(1/e)² независимо от кратности интеграла.

Для сравнения: расчеты по кубатурным формулам р-ого порядка точности для функции m переменных на n шагах по каждой переменной дают количество узлов N=n^m и погрешность расчета e»n^–p. Поэтому число узлов N»(1/e)^m/p экспоненциально растет при повышении кратности интеграла.

[1] Уже известное нам исключение – центральные формулы численного дифференцирования.

[2] Термин «квадратура» обычно используется для численной аппроксимации определенных интегралов, чтобы избежать путаницы с численным интегрированием обыкновенных дифференциальных уравнений.

[3] Можно, конечно, подставлять полиномы вида P_i(x)=xⁱ , но тогда и уравнения, и процесс получения решения будут более громоздкими

[4] В отличие от предыдущих пунктов, для удобства изложения будем нумеровать с i=1, т.е. n – число узлов.

[5] Например, сведением к задаче нахождения корней полинома – см. п. 4.7.1.

[6] Эта формула часто называется формулой Эрмита. Здесь (и далее) использовано название, отвечающее виду ортогональных полиномов, используемых для нахождения узловых точек.

[7] Если с - точка разрыва 1 рода (то есть существуют конечные пределы слева и справа), то исходный первый интеграл можно свести к сумме двух собственных интегралов.