Пределами интегрирования

Способ 1. Если подынтегральная функция f(x) представима в виде произведения f(x)=r(x)×g(x), где r(x) – одна из весовых функций квадратурных формул Гаусса-Лагерра или Гаусса-Эрмита, а g(x) – функция, не имеющая особенностей, то можно использовать соответствующую квадратурную формулу:

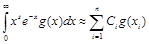или .

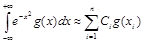Способ 2. Исходный несобственный интеграл разбиваем на сумму двух интегралов

.

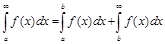Так как исходный интеграл – сходящийся, то всегда можно выбрать число b таким, чтобы для второго интеграла выполнялось неравенство

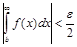, (3.23)

где e – заданная точность вычисления несобственного интеграла.

Тогда, если вычислить первый интеграл (который является собственным), по одной из квадратурных формул, рассмотренных выше, с точностью e/2 , то поставленная задача будет решена.

Таким образом, основная трудность здесь – оценка (3.23). В зависимости от вида подынтегральной функции она проводится или аналитически, или численными методами.

Способ 3. Заменой переменной x=1/t интеграл с бесконечным пределом интегрирования можно свести к интегралу от разрывной функции:

,

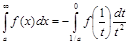приемы интегрирования которого рассмотрены ниже.