ПОЛУЧЕНИЯ КВАДРАТУРНЫХ ФОРМУЛ
Итак, квадратурные формулы имеют вид

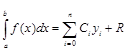 ,
,
причем, как было установлено, если f(x) – полином степени £ n, то эта формула точна (то есть R=0).
Используем это обстоятельство для нахождения коэффициентов квадратурной формулы и ее погрешности.
Будем поочередно подставлять полиномы вида[3]
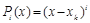 , где 0£ i,k £ n.
, где 0£ i,k £ n.
| i=0: | P0(x)=1; | 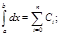
| 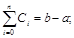
|
| i=1: | P1(x)=x–xk ; | 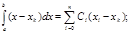
| 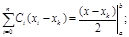
|
| ¼ | ¼ | ¼ | ¼ |
| i=n: | Pn(x)=(x–xk)n; | 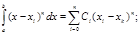
| 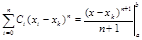
|
Получили систему n+1 линейных алгебраических уравнений для нахождения коэффициентов Сi .
Затем находим погрешность квадратурной формулы тем же способом, что и в п. 3.2 для формул численного дифференцирования.
Продолжаем процесс подстановки полиномов дальше, но уже в квадратурную формулу с погрешностью R ¹ 0:
| i=n+1: | Pn+1(x)=(x–xk)n+1; | 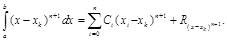
|
Так как коэффициенты Ci уже определены, то из этого уравнения определяем 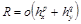 – погрешность квадратурной формулы для полинома вида
– погрешность квадратурной формулы для полинома вида
Pn+1(x)=(x–xk)n+1.
Если погрешность равна нулю, то это означает, что порядок точности формулы выше, и процесс подстановки полиномов продолжается:
Pn+2(x)=(x–xk)n+2 ; Pn+3(x)=(x–xk)n+3;...; Pm(x)=(x–xk)m ,
до тех пор, пока 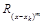 не станет отличной от нуля.
не станет отличной от нуля.
Погрешность квадратурной формулы для произвольной подынтегральной функции находится по формуле
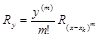 .
.
Пример 6. Получить формулу численного интегрирования на элементарном отрезке по двум точкам:
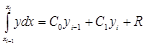 .
.
| y=1: | 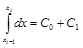 ; ;
| C0+C1=h; |
| y=x–xi : | 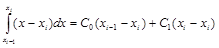 ; ;
| 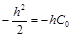 . .
|
Таким образом, С0=C1= h/2, и искомая формула имеет вид:
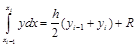 (формула трапеций).
(формула трапеций).
Найдем погрешность.
| y=(x–xi)2 : | 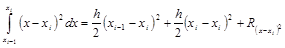 . .
|
Отсюда
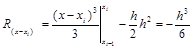 .
. 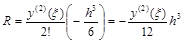 .
.
Пример 7. Получить формулу численного интегрирования на элементарном отрезке по трем точкам:
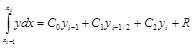 .
.
| y=1: | 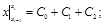
|
| y=(x–xi–1/2): | 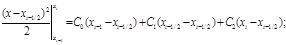 
|
| y=(x–xi–1/2)2: | 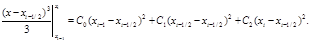
|
Таким образом, система уравнений для искомых коэффициентов имеет вид:
C0+C1+C2 = h;
–C0+C2=0;
C0+C2=h/3.
Решая ее, получаем: C0=h/6; C1=4h/6; C3=h/6.
Найдем погрешность.
| y=(x–xi–1/2)3: | 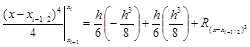 . .
|
Отсюда 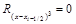 , и процесс подстановки полиномов продолжаем дальше:
, и процесс подстановки полиномов продолжаем дальше:
| y=(x–xi–1/2)4: | 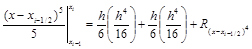 . .
|
Погрешность 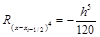 , а
, а
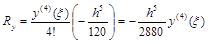 .
.
Таким образом, получили формулу Симпсона:
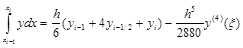 .
.
Пример 8.Получить формулу численного интегрирования, не являющуюся квадратурной в смысле данного определения (п. 3.5):
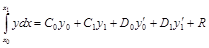 .
.
В правой части стоят производные в узловых точках – в этом отличие данной формулы численного интегрирования от квадратурной формулы интерполяционного типа (см. п. 3.8). Пусть x1–x0=h. Используем метод неопределенных коэффициентов.
| y=1: | h=C0+C1; | Решение: |
| y=x–x0: | h2/2=C1h+D0+D1; | С0=h/2 ; C1=h/2 ; |
| y=(x–x0)2: | h3/3=C1h2+2D1h ; | D0=h2/12 ; D1= –h2/12. |
| y=(x–x0)3: | h4/4=C1h3+3D1h2. |
Погрешность:
y=(x–x0)4: h5/5=C1h4+4D1h3+ 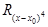 ;
; 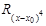 =h5/30;
=h5/30; 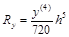 .
.
Следовательно, искомая формула (формула Эйлера) имеет вид:
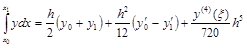 . (3.11)
. (3.11)
Запишем составную формулу Эйлера:
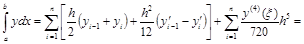
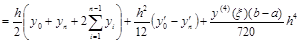 .
.
Таким образом, небольшая добавка к формуле трапеции (а первая группа слагаемых в формуле Эйлера представляет собой именно формулу трапеций) заметно повышает ее точность. Сравните:
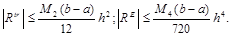
Более того, можно показать, что при численной реализации этой формулы для аппроксимации производных (не снижая точности формулы Эйлера!) можно использовать формулы второго порядка точности:
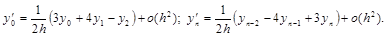
3.8 КВАДРАТУРНЫЕ ФОРМУЛЫ НЬЮТОНА–КОТЕСА
Выше мы рассмотрели квадратурные формулы, основанные на интерполяции подынтегральной функции. Поэтому такие формулы называются также квадратурными формулами интерполяционного типа и в общем случае записываются в виде:
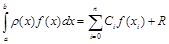 , (3.12)
, (3.12)
где r(х)>0 – заданная интегрируемая функция, называемая весовой функцией.
Если расположение узлов на отрезке интегрирования равномерное, то квадратурные формулы интерполяционного типа называются квадратурными формулами Ньютона-Котеса.
Таким образом, формулы прямоугольников, трапеций, Симпсона являются простейшими частными случаями формул Ньютона-Котеса при r(х)º1.
Основное свойство всех формул Ньютона-Котеса – они точно интегрируют полиномы до степени n включительно. Этот факт мы использовали при работе с методом неопределенных коэффициентов.
Справедливо и обратное утверждение: если квадратурная формула
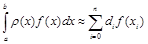
точна для любого полинома степени n , то она является формулой Ньютона-Котеса (или шире – квадратурной формулой интерполяционного типа).
Получим явные выражения для коэффициентов формул Ньютона-Котеса. Это можно сделать простым интегрированием (вот еще один способ построения квадратурных формул) выражения (см. п. 3.5):
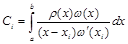 .
.
Заменим переменную x=a+t×h, где t=0,1,..., n.
Тогда:
1) узловые точки x0=a; x1=a+h; x2=a+2h; ... ; xn=a+nh;
2) бином x–xi=a+t×h–a–i×h=h(t–i);
3) полином
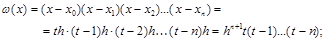
4) производная
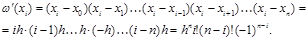
Подставляя все эти выражения в формулу для коэффициентов Сi, имеем:
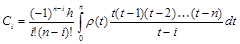 . (3.13)
. (3.13)
Пример 9. Получить коэффициенты квадратурной формулы Ньютона-Котеса при r(х)º1, n=2.
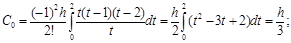
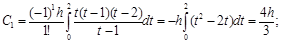
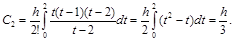
Это коэффициенты квадратурной формулы Симпсона
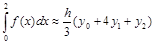 .
.
Погрешность формул Ньютона-Котеса оценивается интегралом от соответствующей погрешности интерполяционного полинома. Используя ту же самую замену переменных, получаем:
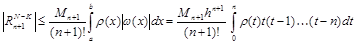 .
.
Отметим, что, как мы уже видели, эта формула не всегда работает (например, для симметричных формул). Тогда следует использовать другие способы определения погрешности.
Примечание. Формулы Ньютона-Котеса высших порядков.
При n = 1, 2, 3, 4, 5, 6, 7, 9 все коэффициенты Ci (3.13) положительны, а при n=8 и n³10 среди них имеются как положительные, так и отрицательные. По этой причине формулу Ньютона-Котеса не рекомендуется применять при больших n.
Конец примечания.
3.9 КВАДРАТУРНЫЕ ФОРМУЛЫ ГАУССА
Рассматривая квадратурные формулы интерполяционного типа, можно сделать вывод, что повышение их точности связано с увеличением количества узловых точек. Зададимся вопросом: нельзя ли повысить точность квадратурной формулы не изменяя количества узлов, а лишь перераспределяя их на заданном отрезке? Ранее мы видели, что можно минимизировать погрешность интерполяционного полинома, выбирая в качестве узлов корни полинома Чебышева. Поэтому есть надежда, что и здесь за счет отказа от равномерного расположения узлов можно получить квадратурные формулы, которые будут точны для полиномов степени выше, чем n.
Поставим задачу так: построить квадратурную формулу

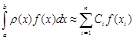 ,
,
которая при заданном n была бы точна для алгебраических полиномов возможно больших степеней m>n. [4]
Воспользуемся методом неопределенных коэффициентов (см. п. 3.7), но будем считать неопределенными не только коэффициенты, но и узлы.
Будем поочередно подставлять в это соотношение полиномы вида
f(x)=xa , где a=0, 1, 2,..., m.
Получим нелинейную систему m+1 уравнений относительно 2n неизвестных С1, С2, ..., Сn, x1, x2,..., xn:
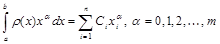 . (3.14)
. (3.14)
Чтобы число уравнений равнялось числу неизвестных, необходимо потребовать m+1=2n. Отсюда m=2n–1 – искомая наивысшая степень алгебраического полинома. Решая эту систему, находим неизвестные С1, С2, ..., Сn, x1, x2,..., xn.
Погрешность найденной квадратурной формулы находим, подставляя в соотношение
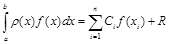
полиномы степени выше, чем m.
Полученные таким образом формулы называются квадратурными формулами наивысшей степени точности или квадратурными формулами Гаусса.
Пример 10. Рассмотрим частный случай. Пусть r(x)º1; a=–1; b=1; n=3. Получим квадратурную формулу вида
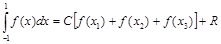 .
.
| f(x)=1; | 2=C(1+1+1) | C=2/3; |
| f(x)=x; | 0=C( 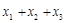 ); );
| 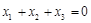 ; ;
|
| f(x)=x2; | 2/3=C( 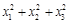 ); );
| 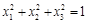 ; ;
|
| f(x)=x3; | 0=C( 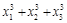 ); );
| 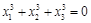 . .
|
Решая систему нелинейных уравнений[5], найдем
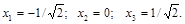
Для нахождения погрешности подставим следующую по порядку функцию f(x).
| f(x)=x4; | 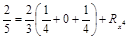 ; ;
| 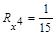 . .
|
Тогда 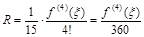 .
.
Таким образом, искомая формула имеет вид:
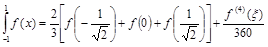 .
.
Такие формулы называются квадратурными формулами Чебышева. Их общий вид:
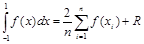 . (3.15)
. (3.15)
При n=8 и n>9 узловые точки xi принимают комплексные значения, поэтому квадратурные формулы Чебышева применимы только для n=1, 2, 3, 4, 5, 6, 7, 9.
Квадратурную формулу Чебышева можно применить и к интегралам с произвольными отрезками интегрирования a и b, сделав замену переменных
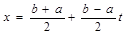 .
.
Эта замена переводит отрезок xÎ[a;b] в отрезок tÎ[–1;1]. Тогда
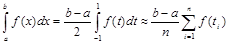 .
.
В общем же случае решение системы (3.14) довольно затруднительно. На помощь приходит теорема, которая дает рекомендации по построению квадратурных формул Гаусса.
Теорема. Квадратурная формула
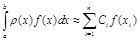 (3.16)
(3.16)
точна для любого полинома степени m=2n–1 тогда и только тогда, когда выполняются два условия:
1) полином w(x)=(x–x1)(x–x2)... (x–xn), составленный по узловым значениям квадратурной формулы x1, x2, …, xn, xÎ [a, b], ортогонален с весом r(х) любому полиному q(x)степени меньшей, чем n, то есть
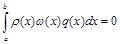 ; (3.17)
; (3.17)
2) формула (3.17) является квадратурной формулой интерполяционного типа, то есть
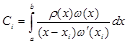 (i=1...n). (3.18)
(i=1...n). (3.18)
Доказательство.
Необходимость. Пусть формула (3.16) точна для любого полинома степени m=2n–1. Тогда она будет точна и для полинома w(x)q(x), так как его степень не выше 2n–1 (полином w(x) имеет степень n, а q(x) имеет степень не больше, чем n–1). Поэтому
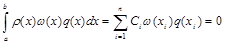 ,
,
так как w(xi)=0 .
Формула (3.17) доказана. А о справедливости (3.18) мы упоминали ранее (п.3.8).
Достаточность. Пусть f(x) – любой полином степени 2n–1. По теореме о делении полиномов его всегда можно представить в виде
f(x)=w(x)q(x)+r(x),
где r(x) – полином степени не выше n–1.
Тогда
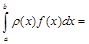
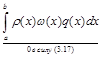
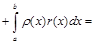
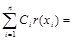
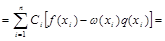
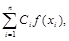
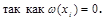
Теорема доказана.
Практический вывод из этой теоремы следующий: чтобы обеспечить наивысший порядок точности квадратурной формулы, необходимо найти систему ортогональных на отрезке [a;b] с весом r(х) полиномов Рn(х) и их корни взять в качестве n узлов х1 ... хn квадратурной формулы. Затем найти коэффициенты квадратурной формулы: либо методом неопределенных коэффициентов, либо непосредственным интегрированием:
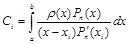 .
.
Для погрешности квадратурных формул Гаусса справедлива формула
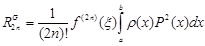 .
.
3.10 НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ КВАДРАТУРНЫХ
ФОРМУЛ ГАУССА
3.10.1 Формула Гаусса-Чебышева[6]
Известно, что полиномы Чебышева Tn(x)=cos(n×arccos(x)) обладают свойством ортогональности с весом 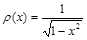 , (–1£x£1).
, (–1£x£1).
T0(x)=1;
T1(x)=x;
T2(x)=2x2–1;
T3(x)=4x3–x;
¼
Tn+1(x)=2xTn(x)–Tn–1(x).
Поэтому справедлива квадратурная формула
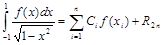 , (3.19)
, (3.19)
где xi – корни полинома Чебышева:
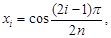
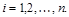
Для коэффициентов Сi,определяя их по формуле
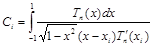 ,
,
получим, что при любом i и n Ci = p/n.
Погрешность формулы можно определить двумя способами: либо методом неопределенных коэффициентов, либо по формуле
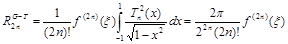 .
.
Таким образом, например, при n=3 формула Гаусса-Чебышева выглядит следующим образом:
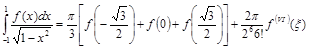 .
.
Дата добавления: 2020-10-25; просмотров: 740;











