АВТОМАТИЧЕСКИЙ ВЫБОР ШАГА ИНТЕГРИРОВАНИЯ

Пусть необходимо вычислить интеграл с заданной предельной погрешностью e, то есть необходимо выполнение условия ½R½£ e . Каким выбрать шаг интегрирования?

Априорную оценку можно получить, потребовав, например, для формулы Симпсона

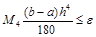, или .

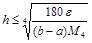На практике такой оценкой пользоваться сложно из-за трудностей оценки четвертой производной.

Поэтому обычно используют апостериорные оценки, например, метод Рунге.

Пусть

,

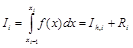где I_h,i – некоторая квадратурная формула, R_i = C_ih^p + o(h^p+1) – погрешность квадратурной формулы, p – порядок точности.

Уменьшим шаг вдвое. Тогда

.

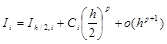Сравнивая эти два соотношения, получаем формулу Рунге для уточнения найденного значения интеграла:

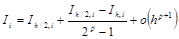
Первое из подчеркнутых слагаемых – главный член погрешности уточненной формулы.

Тогда последовательность действий по выбору шага интегрирования представляется следующей.

Пусть задана точность вычисления e. Проводим по какой-нибудь квадратурной формуле, например, Симпсона (p=4) вычисление интеграла дважды – один раз с шагом h, другой раз с шагом h/2 . По методу Рунге определяем погрешность.

Если оценка

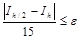
не выполняется, шаг уменьшается еще в два раза, и снова оценивается погрешность

,

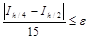и так далее до тех пор, пока не будет выполнено это неравенство. Таким образом, алгоритм сам определяет шаг интегрирования, сообразуясь с заданной точностью. Появляется замечательная возможность – вести интегрирование с крупным шагом на участках плавного изменения функции и с малым шагом на участках более быстрого изменения. Такие алгоритмы называются адаптивными квадратурными алгоритмами.

Отметим, что при реализации таких алгоритмов нет необходимости каждый раз вычислять заново значения функций в узловых точках; достаточно вычислять f(x_i) только во вновь появляющихся узлах. И еще одна рекомендация: необходимо предусмотреть ограничение сверху на число измельчений N, иначе можно доуменьшать до машинного нуля.