Выбор оптимального ассортимента продукции

Применяя изложенный математический аппарат двойственной за­дачи линейного программирования, рассмотрим пример выбора опти­мального ассортимента и объема продукции швейного предприятия. Эта социальная задача сферы сервиса связана с удовлетворением по­требностей населения в бытовых услугах и направлена на улучшение основных производственных показателей эффекта бытового обслужи­вания, заключающегося в снижении стоимости товаров, экономии сво­бодного времени и улучшении качества обслуживания.

Рассмотрим работу швейного предприятия, выпускающего детские костюмы, платья и плащи, сбыт которых зависит от состояния погоды, при этом реализация продукции происходит через фирменные мага­зины.

По данным наблюдений за предшествующие одиннадцать лет пред­приятие в течении апреля — мая в условиях теплой погоды может реа­лизовать 600 костюмов, 2000 платьев и 300 плащей, в условиях про­хладной погоды — 1000 костюмов, 500 платьев и 800 плащей и в усло­виях обычной погоды — 800 костюмов, 1100 платьев и 600 плащей. Затраты на единицу продукции в течение указанных месяцев составили для костюмов 30 ден. ед., для платьев 10 ден. ед. и для плащей 15 ден. ед., а цена реализации равна соответственно 50 ден. ед., 20 ден. ед. и 28 ден. ед.

Задача заключается в максимизации средней величины прибыли от реализации выпущенной продукции с учетом неопределенности по­годы в рассматриваемые месяцы.

Подобная задача рассматривается как игра с природой. Ее отличи­тельная особенность состоит в том, что в ней сознательно действует только один из участников (предприятие), называемый игроком 1. Иг­рок 2 (природа) сознательно против игрока 1 не действует, а выступает как не имеющий конкретной цели и случайным образом выбирающий очередные ходы партнер по игре.

Первоочередной задачей является построение платежной матрицы.

Предприятие располагает тремя чистыми стратегиями: стратегия 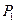с расчетом на теплую погоду, стратегия 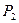с расчетом па прохладную погоду и стратегия 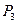с расчетом на обычную погоду.

Природа, рассматриваемая как второй игрок, также располагает тремя стратегиями: обычная погода (стратегия 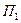), прохладная погода (стратегия 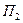) и теплая погода (стратегия ).

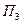Если предприятие выберет стратегию 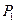то в случае обычной погоды (стратегия природы 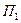) доход составит:

(50 - 30) 600 + (20 - 10)1 100 + (28 - 15)300 - (20 - 10)(2000 - 1000)=

= 17900 ден. ед.,

в случае прохладной погоды (стратегия природы 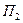) доход будет ра­вен

20 • 600 + 10 • 500 + 13 • 300 - 10(2000 - 500) = 5900 ден. ед.,

и в случае теплой погоды (стратегия природы 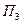) имеем доход, рав­ный

20 • 600+ 10 • 2000 + 13 • 300 = 35900 ден. ед.

Если предприятие выберет стратегию 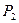, то реализация продукции в условиях обычной погоды дает доход:

. 20 • 800 + 10 • 500 + 13 • 600 - 20(1000 - 800) - 13(800 - 600) =

= 22000 ден. ед.,

в условиях прохладной погоды доход будет:

20 • 1000 + 1.0 • 500 + 13 • 800 = 35400 ден. ед., а в условиях теплой погоды имеем доход:

20 • 600 + 10 -500 + 13 • 300 - 20(1000 - 600) - 13(800 - 300) =

= 6400 ден. ед.

Переходим к решению прямой задачи. Установим соответствие пе­ременных двойственных задач:

C.П. Б.П.

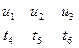
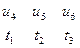
Транспонируем, знаки перед всеми элементами, кроме элементов Z — строки, меняем на обратные, переменные t_j заменяем на соответствующие переменные 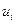, получаем табл. 5.8

Таблица 5.8

п.\.п.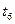
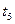
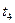
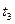
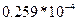
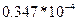
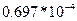
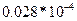
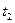
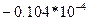
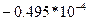
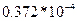
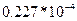
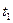
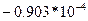
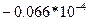
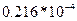
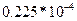
Т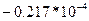

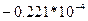
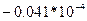
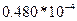
Из табл. 5.8 получаем оптимальное решение. Так как

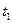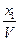, то цена игры V =20833. Из = = 0,225*10⁴

получаем 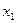- 0.469. Аналогично получим 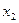= 0,472 и 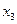= 0,059.

Это означает, что стратегию 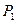нужно применять с вероятностью 0,469, стратегию 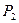— с вероятностью 0,472 и стратегию 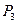— с вероят­ностью 0,059.

Формируем оптимальный план производства:

(600 кост. + 2000 плат, ч- 300 плащ.) • 0,469 +(1000 кост. +

+ 500 плат. + 800 плащ.) • 0,472 + (800 кост. + 1100 плат. +

+ 600 плащ.) • 0,059 = 801 кост. + 1239 плат. + 554 плащ.

Таким обратом, предприятие при производстве 801 костюма, 1239 платьев и 554 плащей получит наибольшую прибыль, кото­рая в сред­нем составит 20833 ден. ед.

Для приведенной формулировки производственной задачи
получили однозначный ответ.

Недостатком данного метода является достаточно большой объем вычислительных операций даже для матрицы с размерностью 3x3. Од­нако, существуют стандартные программы применения симплексного метода на ЭВМ и это снимает подобное неудобство [13].