Верхняя и нижняя цена игры
Рассмотрим платежную матрицу игры 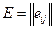 , раскрытую в, виде (рисунок). Здесь i-я строка соответствует
, раскрытую в, виде (рисунок). Здесь i-я строка соответствует 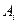 ,-й стратегии игрока A; j-й столбец соответствует
,-й стратегии игрока A; j-й столбец соответствует 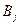 -й стратегии игрока В.
-й стратегии игрока В.
Пусть игрок А выбирает некоторую стратегию 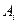 , тогда, в наихудшем случае (например, если выбор станет известен игроку В), ,он получит выигрыш равный
, тогда, в наихудшем случае (например, если выбор станет известен игроку В), ,он получит выигрыш равный 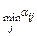 . Предвидя эту возможность, игрок А должен выбрать такую стратегию, чтобы максимизировать свой минимальный в каждой стратегии выигрыш
. Предвидя эту возможность, игрок А должен выбрать такую стратегию, чтобы максимизировать свой минимальный в каждой стратегии выигрыш 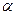 . Таким образом,
. Таким образом,
α= 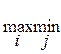 αij (14)
αij (14)
Величина а называется нижней ценой игры (а — это гарантированный выигрыш игрока А). Очевидно а находится в одной из строк матрицы Е, пусть в 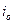 , тогда стратегия А называется максиминной.
, тогда стратегия А называется максиминной.
Итак, если игрок А будет придерживаться максиминной стратегии, то ему при любом поведении игрока В гарантирован выигрыш, во всяком случае не меньший а.
С другой стороны, противник — игрок В, заинтересован в том, чтобы обратить выигрыш игрока А в минимум, поэтому он должен пересмотреть каждую свою стратегию с точки зрения максимального выигрыша игроком А при этой стратегии. Другими словами, при выборе некоторой стратегии 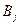 он должен исходить из максимального проигрыша в этой стратегии, равного
он должен исходить из максимального проигрыша в этой стратегии, равного 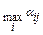 найти такую стратегию, при которой этот проигрыш будет наименьшим, то есть не более, чем
найти такую стратегию, при которой этот проигрыш будет наименьшим, то есть не более, чем
β= 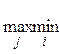 αij (15)
αij (15)
Величина 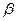 называется верхней ценой игры, а соответствующая ему стратегия
называется верхней ценой игры, а соответствующая ему стратегия 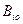 — минимаксной.
— минимаксной.
Принцип осторожности, диктующий игрокам выбор стратегий максиминной ими минимаксной соответственно, в теории игр именуют принципом «минимакса», а сами стратегии максиминные и минимаксные — общим термином «минимаксные стратегии».
Вполне определенной игрой или игрой с седловой точкой называется игра, у которой совпадают нижняя и верхняя цены игры, то есть выполняется равенство:
α= 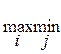 αij =
αij = 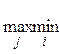 = αij = β (16)
= αij = β (16)
При этом V = а = 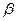 называется ценой игры, а элемент
называется ценой игры, а элемент 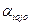 соответствующий равенству, называется седловой точкой.
соответствующий равенству, называется седловой точкой.
Простота решения игры с седловой точкой заключается в том, что оптимальные стратегии обоих игроков находятся сразу. Для игрока А это стратегия 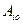 , для игрока В —
, для игрока В — 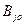 . Причем, такое решение обладает свойством устойчивости в том смысле, что, если один из игроков применяет свою оптимальную стратегию, то любое отклонение другого игрока от оптимальной стратегии может оказаться не выгодным для него.
. Причем, такое решение обладает свойством устойчивости в том смысле, что, если один из игроков применяет свою оптимальную стратегию, то любое отклонение другого игрока от оптимальной стратегии может оказаться не выгодным для него.
Действительно, пусть игрок А выбрал оптимальную стратегию 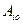 соответствующую α=
соответствующую α= 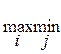 αij =αiojo , то есть игрок А обеспечивает себе выигрыш, равный одному из элементов
αij =αiojo , то есть игрок А обеспечивает себе выигрыш, равный одному из элементов 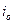 строки, причем, элемент в
строки, причем, элемент в 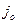 столбце наименьший среди них. И если игрок В выберет j-ю стратегию отличную от
столбце наименьший среди них. И если игрок В выберет j-ю стратегию отличную от 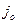 , то он проиграет сумму, равную (
, то он проиграет сумму, равную ( 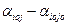 ), а игрок А соответственно выиграет ее. Аналогичные рассуждения показывают невыгодность стратегии, отличной от оптимальной, для игрока А, когда В придерживается своей оптимальной стратегии.
), а игрок А соответственно выиграет ее. Аналогичные рассуждения показывают невыгодность стратегии, отличной от оптимальной, для игрока А, когда В придерживается своей оптимальной стратегии.
Среди конечных игр, имеющих практическое значение, сравнительно редко встречаются игры с седловой точкой. Более типичным является случай, когда нижняя и верхняя цены игры не совпадают ( 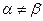 ), причем, нетрудно показать, что тогда
), причем, нетрудно показать, что тогда 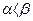 .Действительно, пусть
.Действительно, пусть
α= 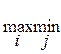 αij =αKS, это означает, что в k-ой строке элемент ,
αij =αKS, это означает, что в k-ой строке элемент , 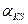 наименьший, то есть при нахождении
наименьший, то есть при нахождении 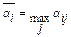 в их число попадут значения не меньшие
в их число попадут значения не меньшие 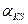 , так как даже в этой строке элементы в других столбцах больше или равны
, так как даже в этой строке элементы в других столбцах больше или равны 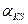 .Значит и
.Значит и
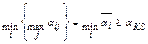
Откуда следует; что 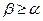 , но мы рассматриваем случай
, но мы рассматриваем случай 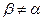 , значит
, значит 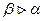 . Итак, в играх не имеющих седловой точки, нижняя цена игры
. Итак, в играх не имеющих седловой точки, нижняя цена игры 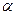 всегда меньше верхней
всегда меньше верхней 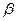 .
.
Установленный факт означает, что если игра одноходовая, то есть партнеры играют один раз, выбирая по одной чистой стратегии, то в расчете на разумно играющего противника они должны придерживаться принципа минимакса, это гарантирует выигрыш 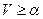 игроку А и проигрыш
игроку А и проигрыш 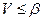 игроку В. Следовательно, при применении минимаксных стратегий величина платежа V ограничена неравенством
игроку В. Следовательно, при применении минимаксных стратегий величина платежа V ограничена неравенством 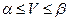 .
.
Если же игра повторяется неоднократно, то постоянное применение минимаксных стратегий становится неразумным. Например, если игрок, В будет уверен в том, что на следующем ходу А применит прежнюю стратегию, то он несомненно выберет стратегию, отвечающую наименьшему элементу в этой строке, а не прежнюю.
Таким образом, мы пришли к выводу, что при неоднократном повторении игры обоим игрокам следует менять свои стратегии. Тогда возникает вопрос: а каким образом их менять, чтобы в среднем выигрыш одного и проигрыш другого был аналогично одноходовой игре, ограничиваясь снизу и сверху соответственно?
Для ответа на этот вопрос введем вероятность (относительную частоту) 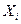 , применения игроком А i-и стратегии, и
, применения игроком А i-и стратегии, и 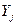 — вероятность применения j-й стратегии игроком В. Совокупности этих вероятностей определяют векторы
— вероятность применения j-й стратегии игроком В. Совокупности этих вероятностей определяют векторы 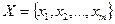 , где
, где
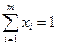 и
и 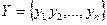 , где
, где 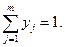
Эти векторы или наборы вероятностей выбора чистых стратегий называются смешанными стратегиями игроков.
В частности, решение игры с седловой точкой дается векторами 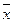 и
и 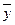 , среди компонент которых
, среди компонент которых 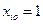 ,
, 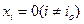 и
и 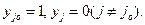
Для получения ограничений на средний выигрыш или проигрыш рассмотрим математическое ожидание выигрыша первого игрока
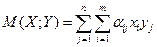 (17)
(17)
Если второй игрок В выбрал некоторую смешанную стратегию У, то первому игроку, естественно, считать лучшей ту смешанную стратегию X, при которой достигается 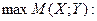
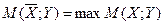
Аналогично, при выборе первым игроком некоторой стратегии X второму игроку следует выбирать стратегию 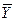 такую, что
такую, что
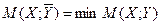
Ясно, что 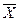 зависит от Y и
зависит от Y и 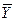 зависит от X. Перед каждым игроком, таким образом, возникает задача выбора оптимальной стратегии, под которой для игрока А понимается смешанная стратегия
зависит от X. Перед каждым игроком, таким образом, возникает задача выбора оптимальной стратегии, под которой для игрока А понимается смешанная стратегия 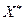 , которая максимизирует математическое ожидание его выигрыша, для игрока В — стратегия
, которая максимизирует математическое ожидание его выигрыша, для игрока В — стратегия 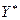 , минимизирующая математическое ожидание его проигрыша.
, минимизирующая математическое ожидание его проигрыша.
Основная теорема теории игр (доказана фон Нейманом в 1928 году) утверждает:
каждая матричная игра с нулевой суммой имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий, то есть существуют стратегии 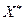 и
и 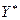 , оптимальные для обоих игроков, причем
, оптимальные для обоих игроков, причем
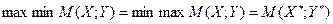
Число 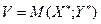 называют ценой игры.
называют ценой игры.
Примечание. Нулевая сумма означает, что выигрыш одного игрока равен проигрышу другого.
Из основной теоремы следует, что каждая конечная игра имеет цену и она лежит между нижней и верхней ценами игры
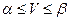
И если одни из игроков придерживается своей оптимальной стратегии, то выигрыш (проигрыш) его остается неизменным независимо от тактики другого игрока, если, конечно последний не выходит за пределы своих «полезных» стратегий, иначе выигрыш (проигрыш) возрастает.
Это означает выполнение неравенств
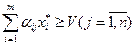 , (18)
, (18)
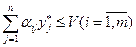
Примечание. Эти неравенства будут необходимы при сведении матричной игры к задаче линейного программирования [13].
5.6.2. Сведение матричной игры к задаче линейного программирования
При наличии неопределенности, причиной которой является присутствие нескольких принципов оптимальности 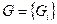 ,
, 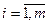 удобно воспользоваться двойственной задачей линейного программирования.
удобно воспользоваться двойственной задачей линейного программирования.
Будем считать, что принципу 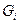 соответствует определенный критерий оптимальности
соответствует определенный критерий оптимальности 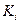 . В качестве
. В качестве 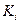 могут выступать: экономические, технические, социальные и иные критерии оптимальности. Показатели
могут выступать: экономические, технические, социальные и иные критерии оптимальности. Показатели 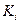 являются функцией управляемых факторов
являются функцией управляемых факторов 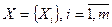 , и неуправляемых факторов
, и неуправляемых факторов 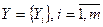 .
.
Итак, набору принципов 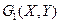 ,
, 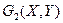 ,...,
,..., 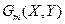 соответствует набор критериев оптимальности
соответствует набор критериев оптимальности 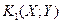 ,
, 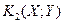 ,…,
,…, 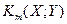 .
.
Располагая множеством критериев 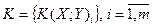 , необходимо определить вектор управляемых переменных
, необходимо определить вектор управляемых переменных 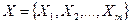 , принадлежащий допустимой области решений X, который обеспечивает оптимальное (в определенном смысле) решение по каждому из частных критериев.
, принадлежащий допустимой области решений X, который обеспечивает оптимальное (в определенном смысле) решение по каждому из частных критериев.
Рассмотрим матрицу игры (2.2.1). Соотношениям отыскания нижней 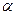 и верхней
и верхней 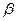 цены игры можно поставить в соответствие эквивалентные им задачи:
цены игры можно поставить в соответствие эквивалентные им задачи:
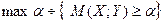 (19)
(19)
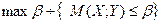 (20)
(20)
где 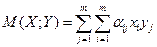 (21)
(21)
есть математическое ожидание выигрыша первого игрока. Тогда для любой чистой стратегии У(j) игрока П.
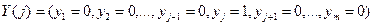
можно записать
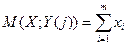 (22)
(22)
а для любой чистой стратегии Х(i) игрока Р
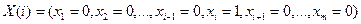
можно записать
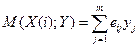 (23)
(23)
Следовательно, задачи (2.6.7) — (2.6.11) допускают следующую запись в форме задач линейного программирования:
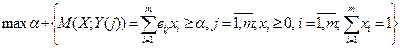
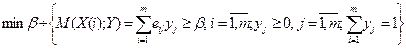 (24)
(24)
Нетрудно видеть, что задачи (5.21) и (5.20) взаимнодвойственные, а поэтому их оптимальные значения должны совпадать, т.е. 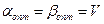 , где V— цена игры (требуемое значение эффективности).
, где V— цена игры (требуемое значение эффективности).
Для задачи (2.6.12) положим:
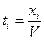 и
и 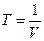 (25)
(25)
а для задачи (2.6.13) положим:
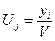 и
и 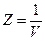 (26)
(26)
Тогда отыскание оптимальной смешанной стратегии 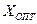 игрока Р приводит к необходимости решения следующей задачи линейного программирования:
игрока Р приводит к необходимости решения следующей задачи линейного программирования:
минимизировать линейную функцию
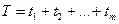 (27)
(27)
при условиях
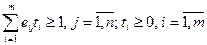 (28)
(28)
а отыскание оптимальной смешанной стратегии 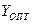 игрока П приводит к необходимости решения следующей задачи линейного программирования:
игрока П приводит к необходимости решения следующей задачи линейного программирования:
максимизировать линейную функцию
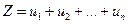 (29)
(29)
при условиях
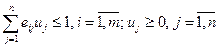 (30)
(30)
Дата добавления: 2020-10-01; просмотров: 861;











