Критерий обобщенного максимина (пессимизма-оптимизма) Гурвица

Критерий Гурвица позволяет учитывать комбинации наихуд­ших со­стояний. Этот критерий при выборе решения рекомендует руково­дствоваться некоторым средним результатом, характери­зующим со­стояние между крайним пессимизмом и безудержным оптимизмом.

В соответствии с этим компромиссным критерием для каждо­го ре­шения определяется линейная комбинация минимального и макси­мального выигрышей.

,

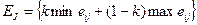и предпочтение отдается варианту решения, для которого ока­жется максимальным показатель 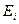т.е.

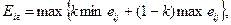(12)

где k - коэффициент, рассматриваемый как показатель оптимизма (О < k < 1).

При k=0 критерий Гурвица совпадает с максимальным критерием, т.е. ориентация на предельный риск, так как больший выигрыш сопря­жен, как правило, с большим риском. При k=1 — ориентация на осто­рожное поведение. Значения k между 0 и 1 являются промежуточными между риском и осторожностью и выбираются в зависимости от кон­кретной обстановки и склонности к риску ЛПР.

Пример. Анализируется матрица полезного результата, имеющая вид табл. 5.4. При значении коэффициента оптимизма k = 0,6 найдем опти­мальную стратегию 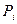. Вычисляем для каждой стратегии линейную ком­бинацию:

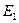= 0,6 • 49 300 + (1 - 0,6) • 197 200 = 108 460,

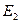= 0,6 • (- 60) + (1 - 0,6) • 297800 =119 084,

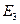= 0,6 • (- 1140) + (1 - 0,6) • 393 600 = 147 756.

Выбираем наибольшее из этих значений:

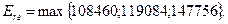
В соответствии с критерием Гурвица средний размер прибыли убу­дет равен 147756 у.е. при выборе объема производства 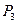= 1 980 000 у.е.

Применительно к матрице рисков R критерий Гурвица имеет вид:

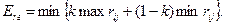(13)

Пример. Рассматривается матрица коммерческого риска, приведен­ная в табл. 5.5. Необходимо определить оптимальную стратегию с по­мощью, критерия Гурвица (5.3.9).

Вычисляем при коэффициенте оптимизма k = 0,6 линейные комби­нации:

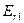= 0,6 • 196400 + (1 - 0,6) • 0 = 117840,

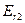= 0,6 • 95800 + (1 - 0,6) • 0 = 57480,

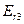= 0,6 • 101000 + (1 - 0,6) • 0 = 60600.

Находим 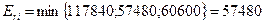, что отвечает вы­бору объема производства 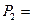1500000 у.е.

Пример. Анализируется матрица выпуска новых видов про­дукции, приведенная в табл. 5.2. Исследовать зависимость 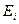от различных значе­ний коэффициента оптимизма k и показать оп­тимальные реше­ния.

Результаты вычислений по формуле (5.8) сведены в табл. 5.6.

Таблица 5.6

Значения показателе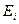й и 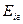для различных k

Решение	Значение коэффициента k
	0,0	0,2	0,4	0,6	0,8	1,0
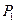
	0,4	0,37	0,34	0,31	0,28	0,25
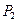
	0,75	0,64	0,53	0,42	0,31	0,2
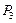
	0,8	0,66	0,52	0,38	0,24	0,1
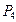
	0,9	0,76	0,62	0,48	0,34	0,2
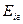
	0,9	0,76	0,62	0,48	0,34	0,25
Оптимальное ре­шение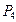

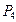
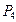
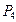
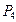
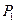
Как видим, с изменением коэффициента k изменяется вариант реше­ния, которому следует отдать предпочтение. Сведем все критерии оп­тимальности в табл. 5.7.

Таблица 5.7

Таблица коэффициентов оптимальности

Показатель	Формула	Название
Наибольшая осторожность		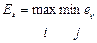Критерий гаранти­рован­ного результата (Вальда)
Наименьшая осторожность		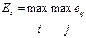Критерий опти­мизма
Крайняя ос­торожность		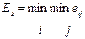Критерий песси­мизма
Минималь­ный риск		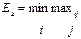Критерий Сэвиджа
Компромисс в решении		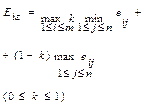Критерий Гурвица
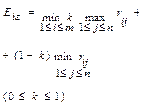
	или	Критерий Гурвица отно­сительно матрицы рисков

5.4. Сравнительная оценка вариантов решений в зависимости от критериев эффективности.

По числу критериев оценки альтернатив выделяют одно- и мно­го­критериальные задачи принятия решения (ЗПР). Принципиаль­ная раз­ница между этими двумя классами задач состоит в том, что в условиях многокритериальное возникает проблема соизмерения, совокупного учета требований разных критериев, которая в Л отличие от задачи упорядочения альтернатив одному единственному критерию не может быть решена формальным путем и требует обращений к ЛПР, органи­зации взаимодействия с ним в процессе решения задачи диалога между человеком и компьютером.

В специальной литературе можно встретить термин «методы реше­ния многокритериальных задач», иногда говорят даже о методах «пре­одоления» многокритериальности. Необходимо иметь в виду, что ка­кого-либо формального математического метода «преодоления» мно­гокритериальности не может быть в принципе. Все без исключения ме­тоды решения многокритериальных задач представляют собой различ­ные способы организации взаимодействия (диалога) с ЛПР и по суще­ству отличаются друг от друга формой вопросов, которые задаются лицу, принимающему решение, в процессе диалогового взаимодейст­вия с ним компьютерной программы.

По числу лиц, принимающих решение, различают задачи индивиду­ального и группового выбора, иначе говоря, задачи с индивидуальным и групповым ЛПР. В особую группу выделяются задачи, в которых возникает проблема интеграции млений разных участников группового ЛПР. Для этого используются различные схемы «голосования», а также менее демократические процедуры, предполагающие наличие так на­зываемого «диктатора».

По кратности решения ЗПР разделяют на уникальные и повторяю­щиеся (типовые). Если ЗПР относится к классу повторяющихся, при оценке целесообразности затрат времени и средств па разработку фор­мальной процедуры ее решения (скажем, компьютеризированной) учи­тывают как прямой эффект — качество решения, так и косвенный — сокращение затрат на выработку решения. Если же речь идет об уни­кальной задаче, весь полезный эффект от использования формального алгоритма будет скорее всего получен за счет повышения качества ре­шения. Следует различать кратность решения задачи и кратность ис­пользования результатов решения. Есть задачи, которые решаются од­нократно, но результаты решения их используются многократно.

Кратность использования результатов предопределяет, в какой форме может формулироваться критерий оптимальности решения. Особенно это относится к условиям риска. Если результат решения ис­пользуется многократно, возможно применение в качестве критерия оценки показателей среднего эффекта (средних ожидаемых затрат, вы­ручки и т.п.). Если же результат используется однократно, то средняя величина эффекта не дает никакого (представления о том, что будет при однократной реализации решения. Более того, кратность реализа­ции решения предопределяет класс стратегий, в котором можно искать решение задачи. При многократной реализации возможно использова­ние так называемых смешанных стратегий, т.е. стратегий, предусмат­ривающих смешивание в определенной пропорции тех или иных дей­ствий. При этом в какой-то доле ситуаций применяется один вариант действия, в другой доле — иной. Совершенно ясно, что апеллирование к таким смешанным стратегиям в случае однократной реализации ре­шения задачи бессмысленно.

Наличие нескольких критериев выбора эффективных альтернатив вносит дополнительную неопределенность при принятии наиболее предпочтительных решений.

Таким образом, имеет место неопределенность двух видов:

1) неопределенность, обусловленная отсутствием или недостатком информации об анализируемых процессах;

2) неопределенность, причиной которой является наличие несколь­ких принципов оптимальности.

Пусть при выборе эффективных решений при наличии неуправляе­мых факторов используется множество критериев оптимальности 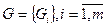. Составляющими 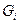могут быть критерии: гарантиро­ванного результата, Сэвиджа, пессимизма и т.д.

Критерии 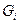являются функцией управляемых факторов

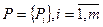и неуправляемых факторов .

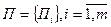Располагая множеством критериев 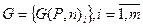необхо­димо выбрать эффективное решение с учетом указанной совокупности решений.

Проанализируем решения примеров, приведенных в этом параграфе.

Анализ выпуска новых видов продукции (табл. 2.2) позволяет выде­лить следующие лучшие стратегии: по критерию гарантированного результата — 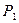, по критерию оптимизма — 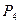, по критерию песси­мизма — 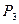, по критерию Сэвиджа — 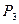, по критерию Гурвица (песси­мизма — оптимизма) при k = 0,6 - .

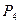Поскольку стратеги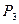и и 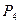фигурируют в качестве оптимальных по два раза, то к практическому применению можно реко­мендовать или стратегию 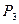или 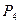. Вместе с тем, стратегия 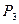является более осторожной и скорее всего ЛПР выберет стратегию .

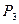Проведем анализ коммерческой стратегии компании при неопреде­ленной конъюнктуре. Исследование матрицы платежеспособного спроса, представленной в табл. 5.4, показывает, что лучшими являются следующие стратегии: по критерию гарантированного результата — 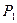, по критерию оптимизма — 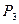, по критерию пессимизма — 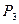, по критерию Гурвица при k = 0,6 - .

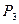Так как стратегия 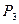повторяется в качестве оптимальной по трем критериям выбора из пяти, то степень ее надежности можно признать достаточно высокой для того, чтобы рекомендовать эту стратегию к практическому применению.

При рассмотрении платежных матриц больших размерностей (m+n — большое) можно быстро, не проводя громоздких вычислительных операций, оценить предлагаемые варианты решений и выбрать из них оптимальный. В этом заключается наиболее существенное преимуще­ство теории оптимальных критериев. Также следует отметить, что имеются стандартные программы для персональных компьютеров, с помощью которых можно исследовать платежные матрицы и находить соответствующие критерии оптимальности.

Из этих примеров видно, что в случае отсутствия информации о ве­роятностях состояний среды теория не дает однозначных и математи­чески строгих рекомендаций по выбору критериев принятия решений. Это объясняется в большей мере не слабостью теории, а неопределен­ностью самой ситуации. Единственный разумный выход в подобных случаях — попытаться получить дополнительную информацию, на­пример, путем проведения исследований или экспериментов. В отсут­ствие дополнительной информации принимаемые решения теоретиче­ски недостаточно обоснованы и в значительной мере субъективны. Хотя применение математических методов в играх с природой не дает абсолютно достоверного результата и последний в определенной сте­пени является субъективным (вследствие произвольности выбора кри­терия принятия решения), оно тем не менее создает некоторое упоря­дочение имеющихся в распоряжении ЛПР данных: задаются множе­ство состояний природы, альтернативные решения, выигрыши и по­тери при различных сочетаниях состояния «среда — решение». Такое упорядочение представлений о проблеме само по себе способствует повышению качества принимаемых решений [13].