Алгоритм оптимального некогерентного приёма
Оптимальный приём при неопределённой фазе и амплитуде сигнала
Рассмотренный ранее способ когерентной обработки сигналов относится к идеализированным условиям, когда не известно, какая из заданных реализаций была передана. При этом форма реализаций, момент прихода и мощность достоверно известны.
Однако в реальных условиях имеет место:
- Изменение параметров канала связи ( 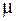 ,
, 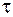 );
);
- Изменение режима передающего устройства
Это приводит к тому, что некоторые параметры реализации сигнала делаются случайными и могут быть оценены с некоторой погрешностью. Такая ситуация особенно характерна для радиоканалов, которые используются в системе связи.
По этому рассматриваемый в данной лекции материал актуален и является базовым для изучения современных радиоприёмных устройств.
Алгоритм оптимального некогерентного приёма
Существует целый ряд каналов связи, в которых фаза сигнала изменяется быстро и получить её точную оценку не удаётся.
В таких ситуациях применяют метод обработки, при котором предполагается, что начальная фаза сигнала не известна и может принимать произвольное значение на интервале ( 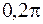 ). Данный метод получил название некогерентный приём.
). Данный метод получил название некогерентный приём.
Будем считать, что сообщение от ИС передаются равновероятно, помехой является БГШ 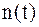 с нулевым средним значением и спектральной плотностью мощности
с нулевым средним значением и спектральной плотностью мощности 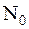 .
.
Оптимальный некогерентный приёмник вычисляет модуль (огибающую) функции взаимной корреляции:
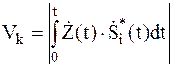 и решает, что был передан тот сигнал, для которого Vk в некоторый момент времени
и решает, что был передан тот сигнал, для которого Vk в некоторый момент времени 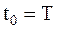 имеет наибольшее значение если
имеет наибольшее значение если 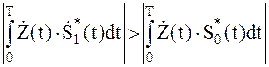 – принимается решение в пользу «
– принимается решение в пользу « 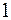 ».
».
Вспомним, что при когерентном приеме вычисляем корреляционный интеграл:
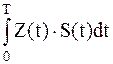 ; ;
| (1.1) |
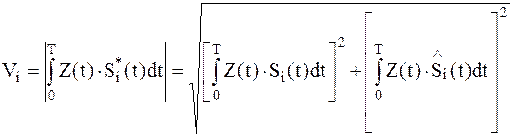 ; ;
| (1.2) |
– т.е. под знаком корень – огибающая сигнала.
Обозначим:
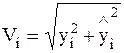 ; ;
| 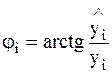 ; ;
| (1.3) |
Предполагаем, что в пределах периода начальная фаза имеет равновероятное значение и 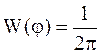

|
В этом случае правило оптимальной обработки принимает вид:
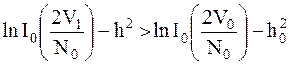 ; ;
| (1.4) |
Если (1.4) выполняется, то решение – в пользу (1.4), где: 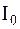 – модифицированная функция Бесселя
– модифицированная функция Бесселя 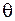 -го порядка. (таблица).
-го порядка. (таблица).
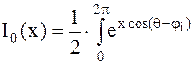 – таблицы – таблицы
| (1.5) |
Дата добавления: 2020-07-18; просмотров: 822;











