Оптимальность по Парето.

Анализ решений при многих критериях в значи­тельной степени сводится к организации в той или иной форме взаимо­действия с ЛПР, которое одно только и может разрешить проблему со­измерения различных критериев. Тем не менее, существует довольно ограниченная область, в которой применение сугубо формального ана­лиза без обращения к ЛПР оказывается весьма полезным. Речь идет о выделении так называемого множества эффективных, или оптималь­ных по Парето, альтернатив.

Легко понять, что альтернатива, не являющаяся эффективной, ни при каких условиях не может рассматриваться в качестве решения задачи. Ведь для неэффективной альтернативы существует другая, превосхо­дящая ее по всем критериям. Отсюда вытекает важнейший критерий рациональности процесса разработки решения: выбираемый вариант должен быть эффективным. Эффективной считается такая альтерна­тива, для которой не существует другой допустимой, не уступающей ей по всем критериям и хотя бы по одному критерию превосходящей ее.

Как же отыскивать эффективные решения? Главное здесь состоит в том, что после того, как сформулированы критерии, задача отыскания множества эффективных решений на заданном множестве альтернатив является, хоть и сложной, но вполне формальной задачей, не требую­щей для своего решая обращения к ЛПР. Во многих случаях множе­ство эффективных альтернатив можно отыскать, решая задачу с инте­гральным критерием оптимальности, представляющим собой сумму отдельных, частных критериев с переменными весами. При этом не имеет значения, какие веса брать для начала процесса. Все равно пере­бираются с каким-то заданным шагом все возможные комбинации на отрезке от 0 до 1. После того, как выделено множество эффективных альтернатив, ЛПР может выбрать одну из них, но строить из них ком­бинации, даже в тех случаях, когда такая комбинированная альтерна­тива имеет смысл, нельзя. Она может оказаться неэффективной и не может рассматриваться в качестве решения задачи.

Мы же отмечали, говоря о различных алгоритмах решения много­критериальных задач что они фактически отличаются друг от друга формой вопросов, задаваемых ЛПР. Очень часто пытаются сформули­ровать эти вопросы таким образом, чтобы ЛПР указало относительные веса (коэффициенты важности или значимости) отдельных критериев, а затем строят так называемую свертку критериев, т.е. за интегральный показатель качества альтернативы принимают сумму отдельных крите­риев с коэффициентами важности.

Такая методика используется настолько часто, что иногда начинает восприниматься как единственно возможная. К ее достоинствам, по­мимо простоты, следует отнести то, что получаемая при таком подходе альтернатива заведомо будет эффективной. Однако применение этой схемы основано на дополнительных предположениях, которые не все­гда оправданы. С математической точки зрения такая сумма частных критериев с коэффициентами важности есть не что иное, как аддитив­ная функция ценности. Для того, чтобы такая логическая конструкция правильно отражала систему предпочтений ЛПР, необходимо (на этот счет доказаны соответствующие теоремы), чтобы используемые для оценки альтернатив критерии обладали свойством взаимной независи­мости по предпочтению.

В пункте (5.3.3) были рассмотрены матрица платежеспособного спроса Е (табл.5.4) и ее матрица рисков R (табл.5.5).

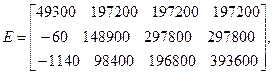
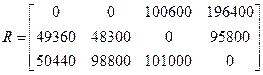
Предположим, что в рассматриваемой схеме известны вероятно­сти 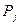того, что реальная ситуация развивается по варианту 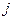.Именно такое положение называется частичной неопределенностью. Тогда ре­шение можно принимать, в частности, по правилу максимизации сред­него ожидаемого дохода.

Пример. Прибыль, получаемая компанией при реализации i-го реше­ния, является случайной величиной 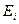с рядом распределения

Математическое ожидание 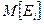и есть средняя ожидаемая

прибыль, обозначаемая также 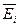. Итак, правило рекомендует при­нять решение, приносящее максимальную среднюю ожидаемую при­быль.

Предположим, что в рассматриваемом примере вероятности равны: 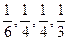. Тогда

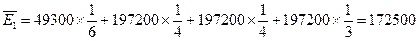
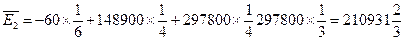
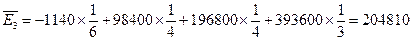
Максимальная средняя ожидаемая прибыль равна 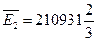и со­ответствует стратегии компании .

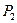Далее рассмотрим выбор решения по правилу минимизации сред­него ожидаемого риска. Риск компании при реализации i-го

решения является случайной величиной 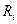с рядом распределения:

Математическое ожидание 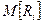и есть средний ожидаемый риск, обозначаемый также 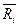.Правило рекомендует принять решение, влеку­щее минимальный средний ожидаемый риск.

Вычислим средние ожидаемые риски при указанных выше вероят­ностях для матрицы рисков R. Получаем:

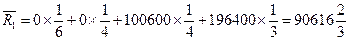
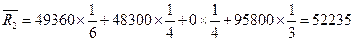
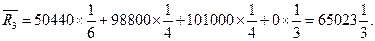
Минимальный средний ожидаемый риск равен 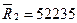и соответ­ствует стратегии компании 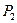. Отличие частичной (вероятност­ной) неопределенности от полной неопределенности очень сущест­венно. Как указывалось выше, принятие решений, исходя из критериев оптимальности, нельзя считать окончательным, самым лучшим. Это лишь некоторые предварительные соображения. Далее пытаются полу­чить дополнительную информацию о возможностях того или иного варианта решения,o его вероятности, что уже предполагает повторяе­мость рассматриваемой схемы принятия решений: то ли это было про­шлом, то ли это будет в будущем.

Итак, в рассмотренном примере была получена оптимизационная двухкритериальная задача по выбору наилучшего решения, так как ка­ждое решение имеет две характеристики — среднюю ожидаемую при­быль и средний ожидаемый риск.

Существует несколько способов постановки таких оптимизационных задач. Рассмотрим один из них в общем виде.

Пусть О — некоторое множество операций. Каждая операция «о» имеет две числовые характеристики Е (о) и К (о) (например, эффектив­ность и риск) и разные операции обязательно различаются хотя бы од­ной характеристикой. При выборе наилучшей операции, желательно, чтобы Е было больше, а R меньше.

Будем говорить, что операция а доминирует операцию в, и обозна­чать а>в, если Е(а) > Е(в) и R(а) > R(в) и хотя бы одно из этих нера­венств строгое. При этом операция а называется доминирующей, а операция в — доминируемой. Ясно, что ни при каком разумном вы­боре наилучшей операции доминируемая операция не может быть при­знана таковой. Следовательно, наилучшую операцию надо искать среди недоминируемых операций Множество этих операций называ­ется множеством Парето или множеством оптимальности по Парето.

На множестве Парето каждая из характеристик Е, R — однозначная функция другой, т.е. по характеристике Е можно определить характе­ристику R и наоборот.

Применительно к матричным играм распределение называется Па­рето — оптимальным, если положение ни одного из игроков нельзя улучшить, не ухудшая при этом положение его партнера.

Продолжим анализ рассматриваемого примера. Каждое решение отметим как точку на плоскости (рисунок), получили

три точки. Чем выше точка , тем более доходная операция, чем точка правее, тем более она рисковая. Значит, нужно выбирать точку выше и левее. В рассматриваемом примере множество Парето состоит только из одной второй операции.

Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу, которая для операции Е с характеристиками 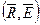дает одно число, по которому и определяют

Множество операций

лучшую операцию. Например, пусть взвешивающая формула имеет вид: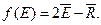

Тогда имеем:

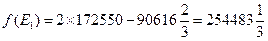
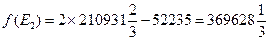
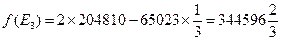
Отсюда видно, что стратегия 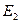— лучшая.

Взвешивающая формула выражает отношение лица, принимающего решение к доходу и риску. Если ЛПР применяет только что рассмот­ренную формулу, то он согласен на увеличение риска операции на две единицы, если доход операции при этом увеличивается не менее, чем на одну единицу. Следует отметить, что эта формула может передать отношение ЛПР к доходу и риску лишь приблизительно.