Z-тест для сравнения выборочной доли со стандартом

Рассмотрим данный параметрический метод сравнения независимых выборок на следующем примере. Допустим, компания получила данные о том, что достаточное количество потребителей предпочтут ее новый продукт. Но на решение о выходе на рынок накладывается еще одно ограничение: компания не будет выводить новый продукт на рынок в случае, если более 50% потребителей будут по-прежнему предпочитать существующий продукт конкурентов. Нулевая и альтернативная гипотеза будут сформулированы следующим образом:

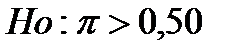
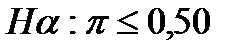
Результаты исследования показали, что 322 респондента из 700 отдали предпочтение конкурентам, так что p=322/700=0,46. Таким образом, вероятно, менее 50% потребителей предпочтут продукцию конкурентов после выхода на рынок, однако необходимо проверить, отличается ли статистически полученное значение (0,46) от стандарта (0,50). Вычисляем по формуле:

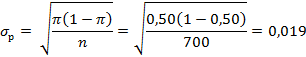
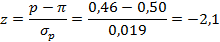
Вероятность (Р) получения z-статистики, равной -2,1 можно из стандартных таблиц (см. Таблицу 2 Приложения). Р=0,9642; 1-Р сравниваем с α. Оно ниже уровня значимости, заданного в исследовании (стандартный уровень значимости α=0,05). Поэтому нулевая гипотеза будет отвергнута и принята альтернативная, которая заключается в том, что после вывода на рынок нового продукта доля потребителей, предпочитающих продукцию конкурентов, не превысит 50%.

Контрольные вопросы и вопросы для самостоятельного изучения

1. Опишите процедуру определения частот распределения значений переменной.

2. Какие показатели центра распределения, вариации и формы распределения вычисляют в ходе обобщения сырых данных анкетирования?

3. Что показывает дисперсия выборочного среднего?

4. Из каких этапов состоит схема проверки гипотезы в маркетинговых исследованиях?

5. Как соотносятся нулевая и альтернативная гипотезы?

6. Что обусловливает выбор метода проверки гипотез об одной переменной?