Малі коливання системи з одним ступенем вільності

Механічна система називається системою з одним ступенем вільності, якщо її положення в просторі може бути однозначно визначене заданням однієї величини q, яку називають узагальненою координатою. Рух системи в просторі описується залежністю узагальненої координати від часу.

При розв’язанні задач положення стійкої рівноваги приймають за нульовий рівень потенціальної енергії.

При складанні диференціального рівняння малих рухів узагальнена координата і узагальнена швидкість за модулем вважаються малими величинами.

Для консервативної системи, з одним ступенем вільності, на яку накладені стаціонарні в’язі, кінетична енергія дорівнює

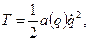(19.7)

де узагальнений коефіцієнт енергії a(q) в загальному випадку є функцією узагальненої координати q. Якщо розкласти a(q) в ряд Маклорена по ступеням q, підставити в формулу (19.7) і відкинути всі складові, починаючи з другої, будемо мати

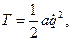(19.8)

потенціальна енергія буде дорівнювати

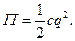(19.9)

Для консервативної системи узагальнена сила

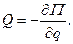
Рівняння руху системи буде таким:

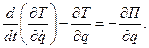
Враховуючи (19.8) і (19.9), при a=const рівняння Лагранжа буде мати вигляд

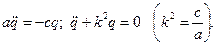(19.10)

Рівняння (19.10) називають диференціальним рівнянням малих коливань системи навколо положення стійкої рівноваги. При розв’язуванні задач на коливання системи з одним ступенем вільності треба:

1) вибрати узагальнену координату q;

2) обчислити кінетичну енергію системи Т через координату q;

3) обчислити узагальнену силу Q через потенціальну енергію;

4) обчислити похідні

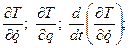
5) скласти рівняння Лагранжа другого роду;

6) знайти необхідні величини.