Теорема про зміну кінетичної енергії тіл при ударі

Якщо удар не абсолютно пружний, то тіла, що співударяються, не відновлюють повністю свою форму в кінці удару. Отже, частина кінетичної енергії, яку мали тіла на початку удару, витрачається на залишкову деформацію, а також на нагрівання тіл. Обчислимо величину кінетичної енергії, яка втрачається при прямому центральному ударі двох тіл, вважаючи, що цей удар не є абсолютно пружним.

Вважаючи, що тіла рухаються поступально, запишемо кінетичну енергію системи на початку удару

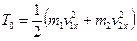(20.36)

і в кінці удару

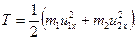(20.37)

Отже, втрата кінетичної енергії при ударі дорівнює

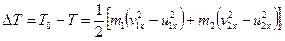(20.38)

Запишемо рівняння, що виражає закон збереження кількості руху:

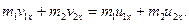(20.39)

Коефіцієнт відновлення

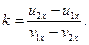(20.40)

Врахувавши рівняння (20.39) і (20.40), з рівняння (20.38) одержимо

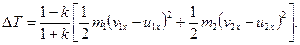(20.41)

Рівняння (20.41) виражає таку теорему:

втрачена при ударі кінетична енергія дорівнює 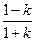- кратній кінетичній енергії втрачених швидкостей.

Справді, ліва частина рівняння (20.41) - це різниця значень суми кінетичних енергій тіл до і після удару, а в правій частині стоять вирази, які за своєю структурою збігаються зі значеннями кінетичних енергій для тих швидкостей, які тіла втрачають при ударі.

Для зручності обчислень формулу (20.41) можна переписати так:

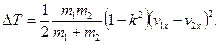(20.42)

Якщо одне з тіл, наприклад, друге тіло, до удару нерухоме (v_2x=0), то

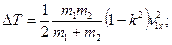
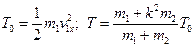. (20.43)

Якщо удар є абсолютно пружним, то k=1 і втрата кінетичної енергії при такому ударі дорівнює нулю. Отже, при абсолютно пружному ударі кінетична енергія не втрачається: кінетична енергія, втрачена за першу фазу удару, коли тіло деформується, повністю відновлюється у другій фазі удару, коли тіла повертають свою початкову форму.

З рівняння (20.41) витікає, що найбільша втрата кінетичної енергії буде при абсолютно непружному ударі (k=0), коли тіла в кінці удару не відновлюють свою початкову форму. В цьому випадку 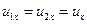і рівність (20.41), що виражає теорему Карно, набирає такого вигляду:

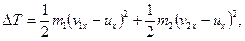(20.44)

тобто кінетична енергія, втрачена системою при прямому центральному абсолютно непружному ударі, дорівнює тій кінетичній енергії, яку мала б система, якби тіла рухались з втраченими швидкостями.

Приймаючи k=0 , з рівняння (20.42) одержимо формулу для втраченої кінетичної енергії при абсолютно непружному ударі в такій формі:

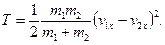(20.45)

Розглянемо випадок, коли v_2x=0. В цьому разі

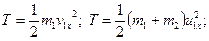(20.46)

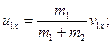(20.47)

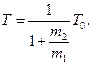(20.48)

Припустимо, що m₂>>m₁ і (m₂ /m₁ )→∞ тоді 1/(1+ m₂ /m₁) →0. При цьому з формули (20.48) витікає, що Т≈0, тобто майже вся кінетична енергія при ударі втрачається і тіла після удару залишаються практично нерухомими. Майже вся кінетична енергія при цьому витрачається на деформацію тіл, що співударяються.

На практиці такий результат використовується при куванні металів. В цьому випадку втрачена кінетична енергія ΔТ= 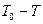іде на деформацію викуваної деталі. Енергія Т, що зберігається після удару і визначається швидкостями, які будуть мати після удару молот і наковальня, є некорисною.

Коефіцієнт корисної дії η молота дорівнює

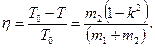(20.49)

З цієї формули видно, що для одержання великого значення коефіцієнта корисної дії маса молота m₁ повинна бути малою величиною в порівнянні з масою m₂ наковальні і деталі, що кується.

Припустимо тепер, що маса m₁ тіла, що ударяє, значно більше маси m₂ тіла, що приймає удар, тоді дріб m₂/m₁ є величиною малою в порівнянні з одиницею і Т₀=T. Таким чином, хоч удар і є абсолютно непружним, кінетична енергія після удару зберігається. Отже, не відбувається і деформації тіл, що співударяються. На практиці такий результат необхідний при забиванні паль, цвяхів і т.д. В цьому випадку корисним є запас кінетичної енергії, який залишається в системі і не переходить в інші форми енергії. Цей запас корисно витрачається на переміщення тіл після удару і на подолання опору. При цьому втрачена корисна енергія ΔT, що йде на деформацію палі, відповідає некорисній роботі. Коефіцієнт корисної дії в цьому випадку дорівнює

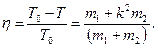(20.50)

Зауваження. Для закріплення матеріалу §20 (пунктів 20.4 і 20.5) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 44.2, 44.3, 44.4, 44.15, 44.22;

2) № 44.5 – 44.7, 44.9, 44.10, 44.11, 44.16, 44.19, 44.21;

3) № 44.13, 44.17, 44.18.

Рекомендується розв’язати також задачі № 16.4 – 16.17, 16.20, 16.27, 16.32 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.