Основне рівняння теорії удару

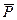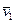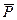Нехай матеріальна точка маси m рухається під дією звичайної не ударної сили . Припустимо тепер, що в момент t₁, коли точка має швидкість , на цю точку починає діяти ударна сила дія якої закінчується в момент t₂. Визначимо рух цієї точки під дією сил і 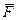за проміжок часу τ =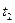 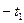, протягом якого триває удар.

Запишемо теорему про зміну кількості руху матеріальної точки:

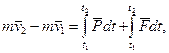(20.1)

де - швидкість точки в момент часу t₂.

За теоремою про середнє значення інтеграла можна записати

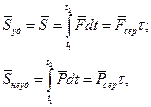(20.2)

де 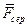і 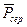- середні значення сил. Добуток ( 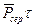) є величиною малою в порівнянні з величиною ( 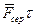), а тому

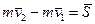. (20.3)

Позначимо швидкість точки на початку удару - 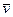, а швидкість точки в кінці удару через 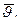Рівняння (20.3) перепишемо так:

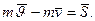(20.4)

Це рівняння виражає теорему про зміну кількості руху матеріальної точки при ударі. Теорему можна сформулювати так: зміна кількості руху матеріальної точки за час удару дорівнює діючому на цю точку ударному імпульсу.

Проектуємо векторну рівність (20.4) на координатні осі

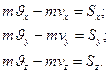(20.5)

Таким чином, зміна проекції кількості руху матеріальної точки на будь-яку нерухому вісь за час удару дорівнює проекції на ту ж вісь діючого на точку ударного імпульсу.

Рівняння (20.4) або (20.5) є основним рівнянням теорії удару і відіграє таку ж роль, як і другий закон динаміки при вивченні рухів під дією звичайних сил.

Розглянемо механічну систему, що складається з n матеріальних точок, і виділимо k-ту точку системи з масою m_k. Запишемо основне рівняння теорії удару для k-тої точки:

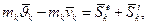(20.6)

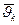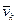де і - швидкості k-тої точки відповідно в кінці і на початку удару, - рівнодійна всіх зовнішніх ударних імпульсів, прикладених до k-тої точки, а - рівнодійна всіх внутрішніх ударних імпульсів, прикладених до тієї ж точки.

Складемо такі рівняння для всіх точок системи і додамо їх почленно. В результаті одержимо

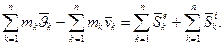(20.7)

Тут 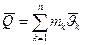і є кількостями руху системи в кінці і на початку удару. В той же час 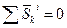на основі рівності дії і протидії.

Таким чином

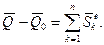(20.8)

Це рівняння виражає теорему про зміну кількості руху системи при ударі, яка формулюється так: зміна кількості руху механічної системи за час удару дорівнює геометричній сумі всіх зовнішніх ударних імпульсів, діючих на цю систему.

Якщ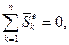о то звідки випливає, що внутрішні ударні імпульси не можуть змінити кількості руху всієї системи.

Проектуючи вектори обох частин рівняння (20.8) на координатні осі, одержимо

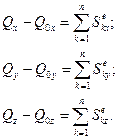(20.9)

Таким чином, зміна проекції на будь-яку вісь кількості руху системи за час удару дорівнює сумі проекцій на цю ж вісь всіх зовнішніх ударних імпульсів, діючих на цю систему. Кількість руху системи дорівнює добутку маси системи на швидкість центра мас системи. Рівняння (20.8) можна записати так:

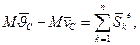(20.10)

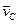де і - швидкості центра мас C системи в кінці і на початку удару, М - маса всієї системи.

Рівняння (20.10) виражає теорему про зміну кількості руху центра мас системи, якщо вважати, що в ньому зосереджена вся її маса: зміна кількості руху центра мас дорівнює геометричній сумі всіх зовнішніх ударних імпульсів, діючих на систему.

Проектуючи вектори обох частин рівняння (20.10) на координатні осі, одержимо

(20.11)

Таким чином, зміна за час удару проекції на будь-яку вісь кількості руху центра мас системи, в якому умовно зосереджена вся її маса, дорівнює сумі проекцій на цю ж вісь всіх зовнішніх ударних імпульсів, діючих на систему.

Позначимо через радіус-вектор k-тої матеріальної точки системи відносно початку О нерухомої (інерціальної) системи відліку. За час відліку положення k-тої точки системи не зміниться, а тому за цей час не зміниться і її радіус-вектор . Запишемо

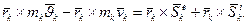
Просумуємо цю рівність по індексу k для всіх точок системи. Врахуємо, що внутрішні ударні імпульси рівні за модулем і прямо протилежні за напрямом, а тому геометрична сума їх моментів відносно будь-якого нерухомого центра дорівнює нулю. В результаті одержимо

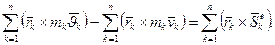
Позначимо кінетичний момент системи відносно центра О на початку удару через 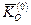, а в кінці удару - через 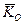, і останнє рівняння запишемо так:

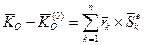
або

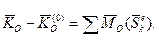(20.12)

Рівняння (20.12) виражає теорему про зміну кінетичного моменту при ударі, яку можна сформулювати так: зміна кінетичного моменту системи відносно будь-якого нерухомого центра дорівнює геометричній сумі моментів всіх зовнішніх ударних імпульсів, діючих на цю систему, відносно того ж центра.

Проектуючи вектори обох частин рівняння (20.12) на координатні осі, одержимо

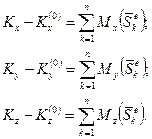(20.13)

Таким чином, зміна кінетичного моменту системи відносно будь-якої нерухомої осі за час удару дорівнює сумі моментів всіх зовнішніх ударних імпульсів, діючих на систему, відносно тієї ж осі.