Вiльнi коливання матерiальної точки при вiдсутностi опору

До коливань вiдносять рухи або процеси, якi повторюються з часом.

За характером залежностi вiд часу фiзичної величини x(t) видiляють перiодичнi коливання, при яких будь-яке значення x(t) повторюється через рiвнi iнтервали часу: x(t)=x(t+T).

Iнтервал (промiжок) часу, протягом якого здiйснюється одне повне коливання, називається перiодом коливань Т.

Величина, обернена до перiоду i рiвна числу коливань за одиницю часу, називається частотою коливань v = 1/T. Частота v коливань вимiрюється в Герцах (Гц): 1 Гц = 1 коливанню за секунду.

Рис. 5. 1.

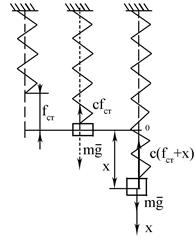Найбiльш важливим видом перiодичних коливань є синусоїдальнi або гармонiчнi коливання. Такi коливання здiйснює тягар на пружинi (рис. 5.1): тут mg - вага тягаря, с - коефiцiєнт жорсткостi пружини, f_ст - статична деформацiя пружини, х - змiщення тягаря вiд положення рiвноваги. У станi спокою вага тягаря зрiвноважена силою натягу деформованої пружини, тому справедлива рівність:

mg = cf_ст. (5.1)

За другим законом Ньютона диференцiальне рiвняння руху тягаря на пружині буде таким:

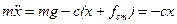
або

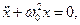(5.2)

де

.

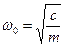Змiщення х тягаря описується диференцiальним рiвнянням другого порядку зi сталими коефiцiєнтами.

Загальний розв’язок рiвняння (5.2) записують у виглядi:

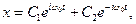(5.3)

де С₁ i С₂ - сталi, якi знаходяться з початкових умов руху. Оскiльки x - дiйсна величина, то С₁ i С₂ повиннi бути комплексними спряженими.

Закон вiльних коливань тягаря на пружинi при вiдсутностi опору можна записати так:

x = Asin(ω₀t) + Bсos(ω₀t) (5.4)

або

x = acos(ω₀t + 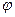₀)(x = asin(ω₀t + 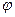₀)). (5.5)

Початковi умови руху записують так:

t₀ = 0; х = х₀;

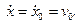
Сталi iнтегрування дорiвнюють:

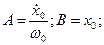(5.6)

.

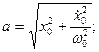
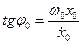Через те, що кожному значенню тангенса вiдповiдають два кути в межах вiд 0 до 2π, то треба визначити ще sinφ₀ i cosφ₀:

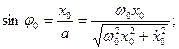
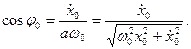(5.7)

Сталу а називають амплiтудою коливань. Амплiтуда дорiвнює розмаху коливань (вiддалi вiд положення рiвноваги до крайнього положення тягаря при коливаннях). Величину (ω₀t+φ₀) називають миттєвою фазою коливань, a φ₀ - початковою фазою. Перiод коливань дорiвнює:

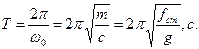(5.8)

Перiод коливань залежить вiд маси тягаря m i коефiцiєнта пружностi с, тобто вiд фiзичних параметрiв коливальної системи, але не вiд амплiтуди коливань.

В той же час величина ω₀ дорiвнює ω₀ = 2π/T = 2π 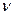i називається циклiчною частотою. Циклiчна частота дорiвнює числу коливань за 2π секунд.

Якщо x(t) - координата тiла, яке здiйснює гармонiчнi коливання, то швидкiсть його 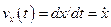i прискорення 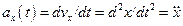змiнюються з часом також за гармонiчним законом:

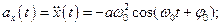
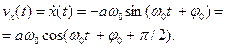(5.9)

Коливання швидкостi випереджають коливання координати по фазi на π/2 (чверть перiоду), а коливання прискорення вiдбуваються в протифазi з коливаннями координати.