Визначення реактивних ударних імпульсів в точках закріплення осі

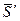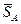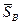Розглянемо тіло, яке може обертатися навколо осі z (рис. 20.1). Нехай АВ=l. Виберемо систему координат з початком в точці А, площину yz проведемо через центр мас С тіла. Якщо на тіло подіє ударний імпульс , то він викличе реактивні ударні імпульси і . Для їх визначення скористаємось теоремами про зміну кількості руху центра мас і кінетичного моменту системи при ударі. При цьому

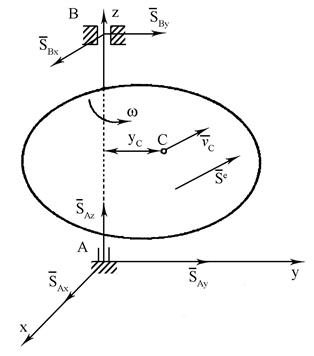
Рис. 20. 1.

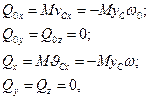(20.14)

де у_С - відстань центра мас тіла від осі обертання, М - маса тіла.

Враховуючи, що в даному випадку ω_x=ω_у=0, а ω_z=ω, маємо

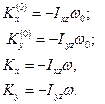(20.15)

Підставимо всі ці значення в рівняння (20.11) і (20.13). В результаті одержимо

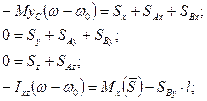(20.16)

де AB=l,

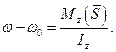(20.17)

Знайдемо, за яких умов всі реактивні ударні імпульси дорівнюють нулю, тобто удар не передається на точки закріплення осі. Якщо точки закріплення осі не зазнають удару, то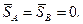

При цьому рівняння (20.16) приймають вигляд

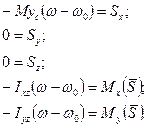(20.18)

З другого і третього рівнянь (20.18) витікає, що для виконання умов 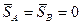необхідно, щоб прикладений ударний імпульс був направлений паралельно до осі х, тобто перпендикулярно до площини yz, яка проходить через вісь обертання і центр мас тіла.

Вибираємо систему координат так, щоб ударний імпульс 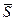лежав в координатній площині хОу (рис. 20.2). Тоді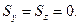

В такому разі

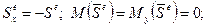
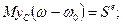(20.19)

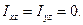(20.20)

З умови (20.20) видно, що вісь обертання z повинна бути для точки О головною віссю інерції.

Крім того, справедлива рівність

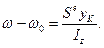(20.21)

З рівнянь (20.19) і (20.21) маємо

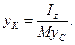(20.22)

Враховуючи, що I_z=Mρ², рівняння (20.22) перепишемо так:

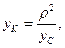(20.23)

де ρ - радіус інерції тіла.

Рис. 20. 2.

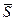Отже, для того, щоб ударний імпульс , прикладений до тіла, що обертається

навколо нерухомої осі, не викликав реактивних ударних імпульсів в точках закріплення осі, необхідні такі умови:

1) ударний імпульс повинен бути розташований в площині хОу, перпендикулярній до осі z, що проходить через точку О тіла, для якої вісь z є головною віссю інерції;

2) ударний імпульс повинен бути перпендикулярним до площини, яка проходить через вісь обертання z і центр мас С тіла;

3) точка прикладання К ударного імпульсу повинна знаходитись від осі z на відстані, що визначається формулою (20.22) або (20.23).

Точка К, через яку при цьому проходить лінія дії ударного імпульсу, що не викликає ударних реакцій в точках закріплення осі, називається центром удару.

Зауваження. Для закріплення матеріалу §20 (пунктів 20.1 – 20.3) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 44.1, 44.23;

2) № 44.20, 44.24, 44.25, 44.26;

3) № 44.27 – 44.29.

Рекомендується розв’язати також задачі № 16.1, 16.2, 16.3, 16.18, 16.23, 16.25, 16.26, 16.42, 16.44, 16.52, 16.53 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Питання для самоконтролю

1. Яке фізичне явище називають ударом?

2. До чого веде удар?

3. На які фази поділяють удар двох тіл?

4. Як змінюється при ударі швидкість тіла?

5. Чим з механічної точки зору характеризується явище удару?

6. Які сили називають ударними? Яка головна особливість цих сил?

7. Що називають часом удару?

8. Які імпульси називаються ударними?

9. Що є мірою механічної взаємодії тіл при вивченні явища удару?

10. Яке рівняння виражає теорему про зміну кількості руху матеріальної точки при ударі? Як формулюється ця теорема?

11. Запишіть основне рівняння теорії удару в проекціях на декартові осі координат.

12. Яку роль відіграє основне рівняння удару в досліджені рухів?

13. Запишіть рівняння, які виражають теорему про зміну кількості руху механічної системи при ударі у векторній формі та у формі проекцій на вісі декартових координат. Сформулюйте цю теорему.

14. Запишіть і сформулюйте теорему про зміну кількості руху центра мас механічної системи та теорему про зміну кінетичного моменту системи при ударі.

15. Напишіть рівняння, які виражають теорему про рух центра мас системи та теорему про зміну кінетичного моменту системи при ударі в проекціях на декартові осі координат.

16. Як визначаються реактивні ударні імпульси в точках закріплення осі тіла при ударі?

17. Які умови відсутності передачі удару на точки закріплення осі тіла?

18. Яку точку називають центром удару?