Визначення положення рівноваги системи. Стійкість рівноваги

Рівновага - такий стан механічної системи, при якому всі її точки перебувають у спокої відносно вибраної системи відліку. Рівновага поділяється на абсолютну (в інерціальних системах відліку) і відносну (в неінерціальних системах відліку). Умови рівноваги визначаються в статиці. Достатньою умовою рівноваги є нульове значення рівнодійної всіх зовнішніх сил і нульове значення головного моменту цих сил (за умови, що початкові швидкості точок дорівнюють нулю, інакше тіло рухатиметься за інерцією).

Розрізняють рівновагу стійку, нестійку та байдужу. Енергетичною ознакою цих видів рівноваги є розташування центра мас системи відносно точки опори чи підвісу: якщо точка опори вища за центр ваги, то тіло має стійку рівновагу (мінімум потенціальної енергії), а при відхиленнях повертається до стану рівноваги. При розташуванні точки опори нижче від центра мас рівновага нестійка: найменше відхилення безпосередньо виводить систему з рівноваги. При збігові названих точок рівновага буде байдужою.

Якщо система, на яку накладені голономні стаціонарні та ідеальні в’язі, знаходиться в консервативному силовому полі, то стійкість рівноваги системи визначається згідно теореми Лагранжа-Діріхле або теореми Ляпунова.

Теорема Лагранжа-Діріхле читається так: якщо в положенні ізольованої рівноваги системи потенціальна енергія має мінімум, то положення рівноваги є стійким.

Потенціальна енергія системи може бути розкладена в ряд за степенями узагальнених координат:

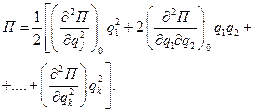(19.1)

Позначимо похідні, які обчислюються в положенні рівноваги, через

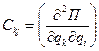. (19.2)

Коефіцієнти C_kj - постійні числа. Перепишемо (19.1) так:

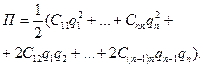(19.3)

Якщо права частина при всіх значеннях q₁, q₂,...,q_n не дорівнює нулю одночасно, то і повна потенціальна енергія П при достатньо малих значеннях q₁, q₂,...,q_n додатна. Це означає, що потенціальна енергія буде мати в положенні рівноваги мінімум.

Згідно теореми Лагранжа - Діріхле в цьому випадку положення рівноваги буде стійким.

Складемо з коефіцієнтів С_kj матрицю:

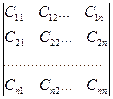. (19.4)

Матриця симетрична:

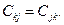
Її головні діагональні мінори такі:

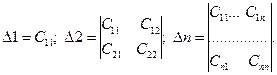(19.5)

За критерієм Сільвестра, якщо всі головні діагональні мінори Δ1, Δ2,...,Δn матриці (19.4) додатні, тобто

Δ1>0; Δ2>0;...Δn>0, (19.6)

то квадратична форма (19.3) додатна.

З теореми Лагранжа-Діріхле виходить, що при виконанні умови Сільвестра положення рівноваги консервативної системи буде стійким. Якщо хоч одна з нерівностей (19.6) не виконується, то на основі першої теореми Ляпунова положення рівноваги буде нестійким.

Для системи з одним ступенем вільності критерій стійкості буде таким:

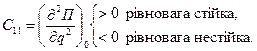
Рівновага є стійкою або нестійкою, якщо при нескінченно малому переміщенні системи з положення рівноваги потенціальна енергія відповідно збільшується або зменшується.

При розв’язанні задач на стійкість рівноваги системи з одним ступенем вільності, що знаходиться під дією потенціальних сил, треба дотримуватись такої послідовності:

1) вибрати узагальнену координату, яка буде визначати положення системи;

2) обчислити потенціальну енергію системи через вибрану узагальнену координату;

3) знайти похідну від потенціальної енергії за узагальненою координатою, прирівняти цю похідну до нуля і знайти можливі положення рівноваги системи;

4) обчислити значення другої похідної від потенціальної енергії за узагальненою координатою для кожного з можливих положень рівноваги, знайти знаки цієї похідної і за ними визначити стійкість рівноваги.