Cистеми числення і способи переведення чисел із однієї системи числення в іншу

Системою числення (численням, нумерацією) називають систему прийомів і правил, що дозволяють встановити взаємно однозначну відповідність між будь-яким числом і його уявленням у вигляді сукупності кінцевого числа символів. Безліч символів, що використовуються для такого уявлення, називають цифрами. Кожній цифрі відповідає певна кількість, що виразима цією цифрою і зветься чисельним значенням або кількісним еквівалентом даної цифри.

Розрізняють непозиційні і позиційні системи числення. В непозиційних системах має місце однозначна відповідність між цифрами і їх кількісними еквівалентами, а будь-яке число визначається як деяка функція від кількісних еквівалентів сукупності цифр, що зображають це число. Якщо як ця функція використовується функція додавання, то систему називають адитивною, якщо ж використовується функція множення, систему називають мультиплікативною. Прикладами непозиційних адитивних систем числення є римська система і одинична (унітарна) система.

Переважне поширення в ЦОТ набули однорідні позиційні системи числення. В такій системі з безпосереднім поданням цифр будь-яке число X виражається у вигляді

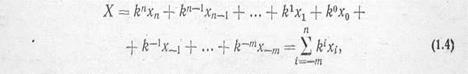де k — основа системи числення, тобто кількість цифр, що використовуються в даній системі (k= 2, 3, ...); х — цифри i-го розряду подання числа в системі з основою k. Величину kⁱ прийнято називати вагою i-го розряду. Оскільки значення k відомо наперед, то вираз (1.4) запишемо в простішій формі

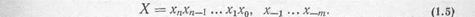
У виразі (1.5) кома відділяє цілу частину числа (n+1 розрядів) від дробової (m розрядів), а вага i-го розряду в k разів більша вага i-1-го розряду. Таку систему числення називають системою з природним порядком ваг.

Неважко помітити, що права частина виразу (1.4) визначає правило обчислення кількісного еквівалента числа, записаного у формі (1.5). На цьому заснований один з алгоритмів переведення чисел з однієї позиційної системи в іншу. Позначимо X(k₁) число в k₁-й системі числення. Для переведення числа в систему з основою k₂ необхідно записати X_(ki) у формі (1.4), замінити цифри x_i і основу k₁ їх k₂-ми уявленнями, а потім виконати операції множення і додавання в системі з основою k₂. Розглянемо приклади.

Описаний спосіб переведення чисел з однієї системи в іншу одержав назву способу безпосереднього заміщення. Найбільше поширення цей спосіб набув у так званому табличному варіанті його реалізації. В цьому випадку в пам’яті ЕОМ зберігаються таблиці k₂-x подання k₁-x цифр і ступенів основи 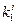. Перевід чисел зводиться до вибірки з цих таблиць k₂-х еквівалентів цифр і ступенів основи, а також до виконання додавання і множення за правилами
k₂-ї арифметики. Цей спосіб зручно використовувати у разі, коли k₁ < k₂ і при переводі чисел в таку систему, де просто виконуються операції додавання і множення (наприклад, із двійкової системи в десяткову).

Приклад 1. Перевести з четвіркової системи в двійкову, а потім у шістнадцяткову число X₍₄₎ — 23013311. У шістнадцятковій системі кількісним еквівалентам 10, 11 15 відповідають цифри А, В, ..., F.

Згідно вищевикладеному

X₍₂₎ = 1011000111110101;

X₍₁₆₎ = B 1 F 5.

Для переведення числа X з канонічної k₁-й системи числення в квазіканонічну систему з основою k₂ спочатку необхідно подати X у канонічній k₂-й системі. Потім ті цифри канонічної k₂-й системи, яких немає в квазіканонічній, замінюють комбінаціями цифр квазіканонічної системи. Після цього за правилами k₂-ї системи підсумовують всі одержані комбінації цифр з урахуванням їх ваг.