Визначення динамічних реакцій в точках закріплення осі тіла, що обертається

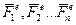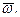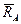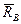Розглянемо тіло, що обертається навколо нерухомої осі під дією заданих активних зовнішніх сил зі змінною за модулем кутовою швидкістю Вісь закріплена в підшипнику В і підп’ятнику А. Модулі і напрями сил реакцій і підп’ятника і підшипника залежать від заданих зовнішніх сил 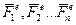і стану руху тіла (рис. 16.1).

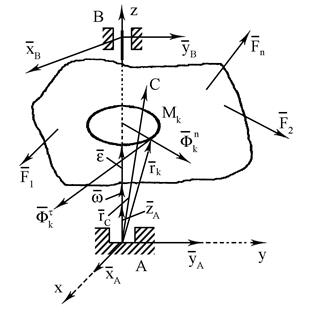
Рис. 16. 1.

Візьмемо початок координат в центрі підп’ятника А. Осі Ox, Oy, Oz пов’язані з ним і, значить, обертаються разом з тілом. Відстань між центрами підп’ятника і підшипника позначимо через h. Реакці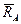ї і 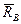розкладемо по осях координат і позначимо їх складові через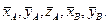

Головний вектор сил інерції дорівнює:

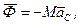
де

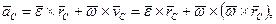(16.1)

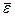- вектор кутового прискорення тіла,

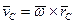- швидкість центра мас С тіла,

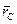- радіус-вектор центра мас.

В такому разі

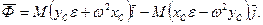(16.2)

Головний момент сил інерції відносно полюса А (центр підшипника А) визначається за формулою:

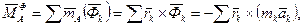(16.3)

де m_k - маса елементарної частини тіла, 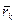- радіус-вектор елементарної частини тіла, 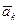- прискорення елементарної частини тіла:

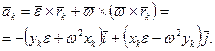
Підставимо останній вираз в формулу (16.3):

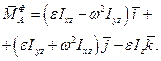(16.4)

Позначимо головний вектор заданих активних зовнішніх сил через 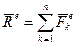і головний момент зовнішніх сил відносно полюса А через 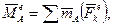тоді згідно принципу Даламбера

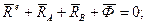
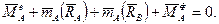(16.5)

Проектуючи векторні рівняння (16.5) на осі координат Axyz, одержимо

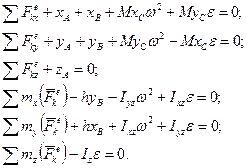(16.6)

Ці рівняння складені по відношенню до рухомих осей, пов’язаних з тілом, а тому тут величини I_xz, I_yz, x_С і у_С є постійними.

Якщо геометрія тіла, розподіл мас і активні зовнішні сили відомі, то розв’язання задач на визначення реакцій 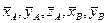можна проводити в такій послідовності:

1) визначимо x_C, y_C, М, I_xz, I_yz,

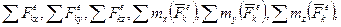
2) з шостого рівняння системи (16.6) визначаємо кутове прискорення, а потім інтегруванням обчислюємо кутову швидкість;

3) підставляємо знайдені значення ω і ε в перші п’ять рівнянь системи (16.6) і знаходимо реакції 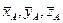підп’ятника А і реакції 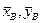підшипника В.

Ці реакції називаються динамічними реакціями. Статичні реакції 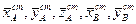визначаються рівняннями:

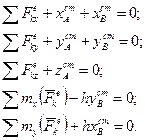(16.7)

Порівнюючи ці вирази з формулами (16.6), помічаємо, що динамічні реакції включають в себе статичні реакції, але мають, крім того, доданки, які називають додатковими динамічними реакціями 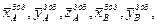що виникають тільки внаслідок обертання тіла.

Представимо динамічні реакції у вигляді

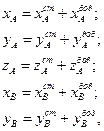(16.8)

з системи рівнянь (16.6) отримаємо такі рівняння для визначення додаткових динамічних реакцій:

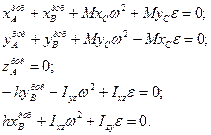(16.9)

З рівнянь (16.6) і (16.9) видно, що для того, щоб динамічні реакції дорівнювали статичним, необхідно і достатньо, щоб при ω≠0 і ε≠0 виконувались такі умови:

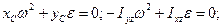
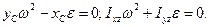(16.10)

Цим рівнянням задовольняють такі значення невідомих:

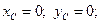(16.11)

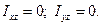(16.12)

Рівності (16.11) показують, що вісь обертання z повинна проходити через центр мас С тіла, а рівності (16.12) показують, що вісь обертання z повинна співпадати з однією з головних осей інерції тіла для точки А. Якщо ці умови виконані, то вісь обертання z є однією з головних центральних осей інерції тіла, і реакції в точках закріплення осі при обертанні тіла, тобто динамічні реакції, не відрізняються від статичних реакцій, які виникають в цих точках при рівновазі тіла під дією тих же активних сил. В такому разі кажуть, що тіло, яке обертається, динамічно зрівноважене на осі обертання, а вісь називають вільною віссю.

Зауваження. Для закріплення матеріалу §16 необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 42.1 - 42.4, 42.7;

2) № 42.5, 42.6, 42.8 – 42.12;

3) № 42.13, 42.15 - 42.18.

Рекомендується розв’язати також задачі № 13.2, 13.4, 13.5, 13.7, 13.8, 13.10, 13.11, 13.14, 13.15, 13.23, 13.25 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Питання для самоконтролю

1. Запишіть, як виражається головний вектор сил інерції через координати центра мас тіла.

2. Як визначається головний момент сил інерції для тіла, що обертається навколо осі, закріпленої в підп’ятнику і підшипнику?

3. Запишіть принцип Даламбера у векторній формі для тіла, що обертається навколо осі, закріпленої в опорах.

4. Як проектуються рівняння принципу Даламбера в цьому випадку на вісі декартових координат?

5. Сформулюйте послідовність розв’язування задач на визначення реакцій опор тіла за допомогою принципу Даламбера.

6. Які реакції називають динамічними реакціями опор?

7. З яких рівнянь визначаються статичні реакції опор?

8. Що називають додатковими динамічними реакціями і чому вони виникають?

9. Як визначаються додаткові динамічні реакції опор?

10. За яких умов статичні і динамічні реакції опор дорівнюють між собою?

11. Коли тіло, що обертається, вважають динамічно зрівноваженим на осі обертання?

12. В якому випадку вісь обертання тіла називають вільною віссю?