Можлива робота сили. Ідеальні в'язі. Узагальнена сила

Розглянемо механічну систему з голономними в’язями. Нехай на довільну матеріальну k-ту точку системи діє сила 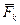, рівна сумі всіх діючих на цю точку сил. Робота цієї сили на можливому переміщенні 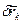обчислюється за формулою

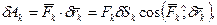(17.12)

де враховано що за модулем вектор 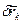дорівнює елементу дуги 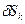траєкторії, яку описує k-та точка при можливому переміщенні, тобто 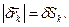Формулу (17.12) в проекціях на вісі x, y, z можна записати у вигляді

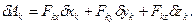(17.13)

Рівняння (17.13) справедливе для кожної матеріальної точки системи. Додаючи їх почленно, одержимо для системи таке рівняння:

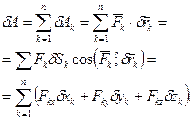(17.14)

При переході до узагальнених координат врахуємо:

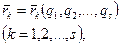(17.15)

де s - число ступенів вільності системи. Розкладаючи функцію в ряд Тейлора і утримуючи лише члени першого порядку малості, можна можливе переміщення 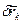(k=1,2,..., n) будь-якої точки системи представити через незалежні одна від одної варіації 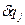(j=1,2,...,s) узагальнених координат 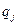(j=1,2,...,s) у вигляді

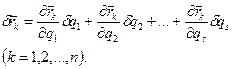(17.16)

З рівнянь (17.14) і (17.16) одержимо

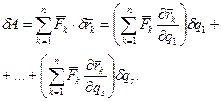(17.17)

Введемо позначення:

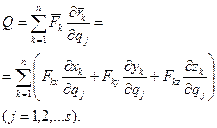(17.18)

В такому разі можлива елементарна робота δА в узагальнених координатах буде дорівнювати

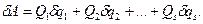(17.19)

Ця формула по своїй структурі нагадує формулу (17.13). Коефіцієнти Q₁, Q₂,...,Q_s в формулі (17.19) називаються узагальненими силами.

Надамо системі таке можливе переміщення, при якому змінюється тільки одна узагальнена координата, наприклад q₁, a решта координат залишаються незмінними , тобто

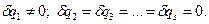
Позначимо суму можливих робот сил 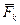на цьому переміщенні через δА'. Тоді

,

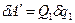і

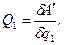(17.20)

У випадку, коли всі діючі на систему сили (зовнішні і внутрішні) є консервативними, узагальнені сили обчислюються за формулою:

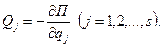(17.21)

Число узагальнених сил дорівнює числу узагальнених координат, яке в свою чергу дорівнює числу ступенів вільності голономної системи.

Розмірність узагальненої сили залежить від відповідної узагальненої координати:

[Q_j]=[poбoтa]/q_j.

В якості прикладу розглянемо кривошипно - шатунний механізм (рис. 17.3).

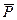На повзун В діє сила , до кривошипа ОА=r прикладений момент опору М. Обчислимо узагальнену силу. Механізм має один ступінь вільності.

Рис. 17. 3.

Надамо системі можливе переміщення і запишемо вираз для можливої роботи всіх сил:

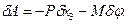
Варіація δх₃ не є незалежною варіацією. З рис. 17.3 маємо

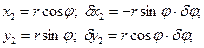
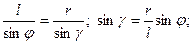
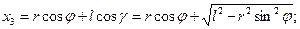
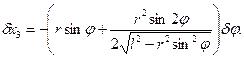
Елементарна робота дорівнює

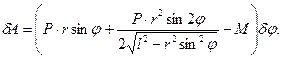
Звідси

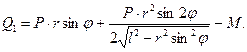
Ідеальними називаються такі в’язі, для яких сума елементарних робот всіх реакцій в’язей на всякому можливому переміщенні системи дорівнює нулю, тобто

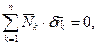(17.22)

де 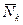- реакція в’язі, діюча на k-ту матеріальну точку системи,

n - число матеріальних точок в даній системі.

Прикладами ідеальних в’язей є:

1) абсолютно гладенькі поверхні і лінії (направляючі);

2) абсолютно тверда жорстка поверхня при перекочуванні по ній абсолютно твердого тіла без ковзання;

3) ідеальні шарніри і підшипники.