Елементарна теорія гіроскопічних явищ

Гіроскопом називають тверде тіло, яке має вісь симетрії і обертається навколо цієї осі з кутовою швидкістю, що значно більша за кутову швидкість обертання самої осі симетрії.

У сучасних гіроскопах кутова швидкість власного обертання гіроскопа (обертання тіла навколо осі симетрії) ω₁ досягає значення 6·10⁴ с^-1 , в той же час кутова швидкість обертання осі ω₂≈1·10^-2 с^-1. Це значить, що кінетичний момент гіроскопа можна обчислити за формулою:

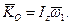(14.22)

В елементарній теорії гіроскопічних явищ виходять з таких припущень:

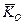а) кінетичний момент гіроскопа відносно його точки О направлений по осі симетрії гіроскопа Oz;

б) модуль кінетичного моменту дорівнює добутку моменту інерції гіроскопа відносно його осі симетрії та кутової швидкості його власного обертання.

Розглянемо зрівноважений або вільний гіроскоп. Гіроскоп, на який не діють зовнішні сили або ці сили зрівноважені, називається зрівноваженим або вільним гіроскопом (рис. 14.3).

Рис. 14.3

Якщо на гіроскоп не діють зовнішні сили, то

Рис. 14. 3.

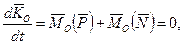(14.23)

звідси

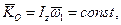(14.24)

тобто модуль і напрям кінетичного моменту 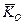вільного гіроскопа відносно точки опори є постійним; вектор 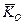направлений по осі гіроскопа. Це значить, що вісь вільного гіроскопа зберігає незмінний напрям в просторі по відношенню до інерціальної (зоряної) системи відліку.

З рівності (14.24) зокрема витікає, що вільний гіроскоп обертається з постійною кутовою швидкістю 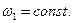В дійсності кутова швидкість 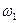зменшується, бо тут не врахований опір повітря і сили тертя в точці опори.

Знайдемо, куди буде відхилятись вісь гіроскопа, якщо до неї прикласти паралельно до осі Оу силу 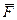(див. рис. 14.3). Момент сили 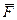відносно точки опори О дорівнює за модулем 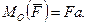Згідно теореми Резаля маємо:

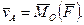(14.25)

Таким чином, якщо на вісь гіроскопа, що швидко обертається, подіє сила, то ця вісь буде відхилятись за напрямком, який має вектор - момент цієї сили відносно точки опори гіроскопа.

Рис. 14. 4.

Розглянемо гіроскоп, у якого вісь динамічної симетрії Oz не є вертикальною, а утворює в початковий момент часу кут θ з вертикальною віссю Oz₁, при цьому нерухома точка О не співпадає з його центром ваги С (рис. 14.4).

Головний момент зовнішніх сил дорівнює:

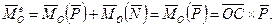(14.26)

Тоді

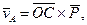(14.27)

а значить, вісь Oz гіроскопа обертається навколо вертикальної осі Oz₁, тобто здійснює регулярну прецесію.

Обчислимо кутову швидкість ω₂ прецесії. З (14.27) маємо:

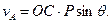(14.28)

З іншого боку, швидкість точки А (кінець вектора 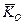) можна знайти за формулою:

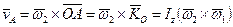(14.29)

або

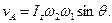(14.30)

З формул (14.28) і (14.30) знайдемо:

;

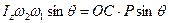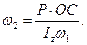(14.31)

Таким чином, чим швидше обертається гіроскоп, тим повільніше він прецесує, і навпаки, - чим повільніше обертається гіроскоп, тим швидше він прецесує.

Дослідимо гіроскопічний ефект. Для цього розглянемо гіроскоп, який обертається з кутовою швидкістю 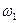навколо горизонтальної осі Oz, закріпленої за

Рис. 14.5допомогою підшипників В₁ і В₂в рамі, яка в свою чергу обертається з кутовою швидкістю 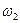навколо вертикальної осі Oz₁ (рис. 14.5).

Нехай 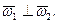В цьому випадку:

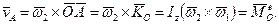(14.32)

Рис. 14. 5.

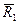Цей момент створюють сили і 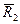, з якими підшипники В₁ і В₂ тиснуть на вісь гіроскопа. В свою чергу, вісь гіроскопа буде тиснути на підшипники В₁ і В₂з силами 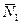і 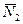, рівними за модулем і направленими протилежно до сил 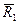і 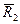. Пара сил ( 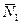; 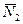) називається гіроскопічною парою, а її момент 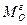, рівний за модулем 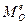, але направлений в протилежний бік, називається гіроскопічним моментом.

Ефект дії гіроскопічної пари ( 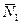; 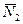) на підшипники, в яких закріплена вісь гіроскопа, називається гіроскопічним ефектом.

Оскільки 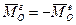, то

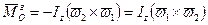, (14.33)

за модулем

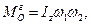(14.34)

бо

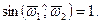
Для визначення N₁ або N₂ треба скористатись рівністю:

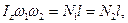(14.35)

тобто

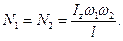(14.36)

Якщо поворот проводиться швидко (ω₂ є великою величиною), то гіроскопічний тиск може бути великим і зруйнувати підшипники. Ось чому величини цих тисків повинні враховуватись при відповідних розрахунках підшипників.

Крім гіроскопічних (динамічних) тисків на підшипники В₁ і В₂, будуть діяти статичні тиски 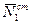і ( рис. 14.6 ):

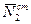Рис. 14. 6.

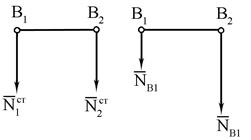
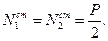(14.37)

Тоді

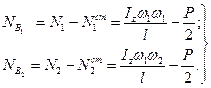(14.38)

Зауваження. Для закріплення матеріалу §14 (пункт 14.5) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 40.1, 40.2, 40.3, 40.5;

2) № 40.4, 40.6 – 40.9;

3) № 40.10, 40.11.

Рекомендується розв’язати також задачі № 15.5, 15.6, 15.7, 15.16, 15.18, 15.19, 15.23, 15.25, 15.29, 15.31 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Питання для самоконтролю

1. Яке тверде тіло називають гіроскопом?

2. Як співвідносяться в сучасних гіроскопах кутова швидкість власного обертання гіроскопа і кутова швидкість обертання осі?

3. Як обчислюють кінетичний момент гіроскопа?

4. Які припущення вводять в елементарній теорії гіроскопічних явищ?

5. Який гіроскоп називається зрівноваженим або вільним?

6. Яким є модуль і напрям кінетичного моменту вільного гіроскопа відносно точки опори?

7. Як змінюється напрям осі вільного гіроскопа в просторі по відношенню до інерціальної системи відліку?

8. Який висновок можна зробити, розглянувши формулу кінетичного моменту вільного гіроскопа?

9. Куди буде відхилятись вісь гіроскопа, якщо до неї прикласти силу?

10. Як визначається головний момент зовнішніх сил, прикладених до гіроскопа, у якого вісь динамічної симетрії утворює кут Θ з вертикальною віссю, а нерухома точка не співпадає з центром ваги гіроскопа?

11. Як рухається вісь Оz такого гіроскопа?

12. Як визначається кутова швидкість прецесії гіроскопа?

13. Поясніть, як пов’язане обертання гіроскопа з його прецесією.

14. Яку пару сил називають гіроскопічною парою?

15. Який момент називають гіроскопічним моментом?

16. Що називають гіроскопічним ефектом?

17. Як визначається гіроскопічний момент?

18. Запишіть, як визначаються динамічні тиски осі гіроскопа на підшипники, в яких вона закріплена.

19. Чому потрібно враховувати гіроскопічний тиск на підшипники?

20. Як визначаються статичні тиски на підшипники, в яких закріплена вісь гіроскопа?