Принцип Даламбера. Метод кінетостатики

Принцип Даламбера є одним з основних принципів механіки, який використовують для розв’язання другої задачі динаміки невільної матеріальної точки і матеріальної системи. За основним рівнянням динаміки матеріальної точки маємо:

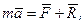(15.1)

де 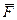- рівнодійна прикладених до точки сил, 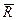- рівнодійна реакцій в’язей.

Рівняння (15.1) запишемо так:

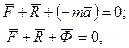(15.2)

де 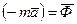- сила інерції матеріальної точки.

Сила інерції матеріальної точки дорівнює добутку маси точки та її прискорення і направлена протилежно прискоренню.

Сили інерції - фіктивні сили, які штучно вводяться для спрощення задач в інерціальних системах (даламберові сили інерції) або для збереження законів динаміки Ньютона в неінерціальних системах відліку (ейлерові сили інерції).

Даламберові сили інерції - це сили протидіючого характеру 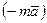, перенесені з прискорюючого тіла на прискорюване, де фактично їх немає.

Ейлерові сили інерції є проявом інертності тіл на фоні неінерціальної системи відліку.

На основі формули (15.2) принцип Даламбера формулюється так: якщо до активних сил, які діють на матеріальну точку, додати реакції в’язей і сили інерції, то вся система сил перебуватиме в рівновазі. Принцип Даламбера дає можливість звести задачі про рух невільної матеріальної точки до задач статики.

Якщо прискорення точки

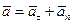, то

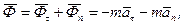(15.3)

де 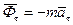- дотична сила інерції, 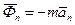- нормальна сила інерції.

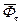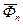Модулі векторів і дорівнюють:

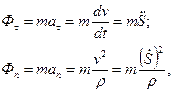(15.4)

де S - дугова координата, ρ - радіус кривизни траєкторії.

При обертальному русі твердого тіла сили інерції частинки M_k тіла масою m_k визначаються так:

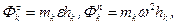(15.5)

де h_k - відстань від частинки M_k тіла до осі обертання.

Як і для матеріальної точки, диференціальним рівнянням руху матеріальної системи можна надати форму рівнянь статики.

Для матеріальної точки M_k системи запишемо:

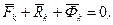(15.6)

де 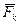і 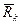- відповідно рівнодіючі активних сил і реакцій в’язей, діючих на точку M_k , 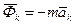- сила інерції точки M_k (m_k – маса точки і 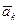- прискорення точки).

Сумуючи (15.6) по всій системі точок і вводячи позначення

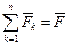- головний вектор активних сил,

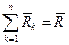- головний вектор реакцій в’язей,

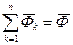- головний вектор сил інерції, отримаємо:

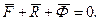(15.7)

Рівняння (15.6) помножимо векторно на радіус - вектор 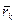точки M_k відносно будь-якого центра О і просумуємо по всій системі точок:

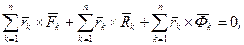
тут 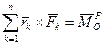- головний момент активних сил відносно центра О;

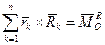- головний момент реакцій в’язей відносно центра О;

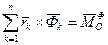- головний момент сил інерції відносно центра О.

Тоді

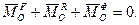(15.8)

На основі рівнянь (15.7) і (15.8) принцип Даламбера для матеріальної системи формулюється так: в кожний момент часу сума головних векторів активних сил, реакцій в’язей і сил інерції, а також сума головних моментів відносно будь-якого центра О активних сил, реакцій в’язей і сил інерції дорівнюють нулю.

Векторним рівнянням (15.7) і (15.8) відповідають шість рівнянь в проекціях на осі декартових координат:

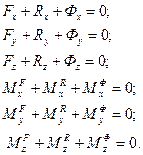(15.9)

Використання метода кінетостатики для твердого тіла потребує уміння розраховувати головний вектор і головний момент його сил інерції.

Розглянемо різні види руху твердого тіла.

1) Тверде тіло рухається поступально:

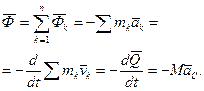(15.10)

Таким чином, при поступальному русі сили інерції точок твердого тіла зводяться до рівнодіючої сили, прикладеної в центрі мас тіла, рівною за модулем добутку маси тіла та модуля прискорення його центра мас і направленої протилежно цьому прискоренню.

2) Обертання твердого тіла, що має площину матеріальної симетрії, навколо нерухомої осі, перпендикулярної до цієї площини. При обертанні твердого тіла, що має площину матеріальної симетрії, навколо осі, перпендикулярної до цієї площини ( рис. 15.1, а), сили інерції точок тіла зводяться до рівнодіючої сили, яка лежить в площині симетрії.

Модуль і напрям цієї сили визначається формулою:

,

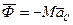де 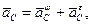(15.11)

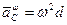- доцентрове прискорення,

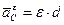- обертальне прискорення,

d – відстань від центра мас до осі обертання,

ω і ε - відповідно кутова швидкість і кутове прискорення обертання твердого

Рис. 15.1, а,бтіла.

Головний вектор 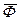прикладений в точці О (рис. 15.1,б). Лінія дії сили 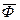відстоїть від точки О на відстані

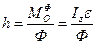, (15.12)

де I_z - момент інерції твердого тіла відносно осі обертання.

Якщо вісь обертання є центральною (проходить через центр мас С тіла), то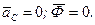

В той же час

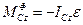, (15.13)

де I_Cz - момент інерції тіла відносно осі обертання.

3) Плоский рух твердого тіла, що має площину матеріальної симетрії.

Такий рух твердого тіла складається з поступального руху і обертального навколо рухомої осі Cz₁ , яка проходить через центр мас перпендикулярно до площини симетрії.

Рис. 15. 1.

В цьому разі сили інерції поступального руху тіла зводяться до сили, прикладеної в центрі мас, яку обчислюють за формулою:

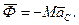(15.14)

Сили інерції обертального руху тіла зводяться до пари сил, яка лежить в площині симетрії, з моментом пари:

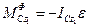. (15.15)

Застосовуючи метод кінетостатики до рухомої матеріальної точки, треба записати умови рівноваги активних сил, реакцій в’язей і сил інерції у формі (15.2) або (15.3). З одержаних рівнянь обчислити шукану величину.

Якщо об’єктом дослідження руху є тверде тіло, то, застосовуючи метод кінетостатики, треба скласти рівняння рівноваги системи сил, включивши до них активні сили, реакції в’язей і сили інерції. Розв’язування задач за допомогою методу кінетостатики слід виконувати в такій послідовності:

1) показати на рисунку активні сили, прикладені до кожної матеріальної точки або твердого тіла;

2) застосувати закон про звільнення від в’язей і показати реакції в’язей, накладених на кожну з матеріальних точок системи;

3) визначити сили інерції, показати їх напрям;

4) вибрати систему координат;

5) скласти рівняння рівноваги для кожної матеріальної точки системи або твердого тіла;

6) розв’язати складену систему рівнянь, обчислити шукані величини.

Зауваження. Для закріплення матеріалу §15 необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 41.1 - 41.4, 41.7, 41.10, 41.11;

2) № 41.9, 41.12, 41.13, 41.14, 41.16, 41.17 – 41.19;

3) № 41.20, 41.21, 41.22, 41.23.

Рекомендується розв’язати також задачі № 878, 879, 885, 886, 888, 889 - 892 зі збірника “Сборник задач по теоретической механике /Под ред. М. А. Бражниченко. – М., Высшая школа, 1986”.

Питання для самоконтролю

1. Для чого використовують принцип Даламбера?

2. В чому полягає принцип Даламбера?

3. Запишіть рівняння, яке відповідає принципу Даламбера для матеріальної точки.

4. Як визначається сила інерції матеріальної точки?

5. Що називають даламберовими та ейлеровими силами інерції? Для чого вони вводяться?

6. Як принцип Даламбера полегшує розв’язання задач про рух невільної матеріальної точки?

7. Як визначаються дотична і нормальна сили інерції?

8. Як визначаються сили інерції частинки тіла при його обертальному русі?

9. Запишіть і сформулюйте принцип Даламбера для механічної системи.

10. Запишіть рівняння в проекціях на осі декартових координат, що відповідають векторним рівнянням принципу Даламбера для матеріальної системи.

11. До чого приводяться сили інерції точок тіла, яке рухається поступально?

12. До чого зводяться сили інерції точок тіла, яке обертається навколо нерухомої осі, перпендикулярної до його площини матеріальної симетрії?

13. Запишіть, як визначаються модуль і напрям рівнодіючої сил інерції у випадку обертання тіла навколо нерухомої осі.

14. Де прикладений головний вектор сил інерції у випадку обертального руху твердого тіла?

15. На якій відстані від осі обертання проходить лінія дії головного вектора сил інерції тіла?

16. Як визначається головний момент сил інерції, якщо вісь обертання є центральною віссю інерції?

17. До чого зводяться сили інерції у випадку плоского руху твердого тіла? Запишіть відповідні формули.

18. Як використовують принцип Даламбера для розв’язання задач?