Диференціальні рівняння плоского руху твердого тіла

<23 24 252627 28 29 >

Плоский рух твердого тіла складається з поступального разом з полюсом – центром мас С – в площині руху, і обертального навколо осі Cz, яка проходить через центр мас і перпендикулярна до нерухомої площини. А тому згідно з пунктами 14.1 і 14.2 диференціальними рівняннями плоского руху твердого тіла будуть:

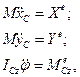(14.5)

де

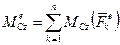При розв’язанні задач треба дотримуватись такого порядку:

1) вибрати систему відліку Оху в площині плоскої фігури;

2) розглянути тіло в деякому положенні і прикласти до нього зовнішні сили;

3) накладені в’язі замінити їх реакціями;

4) скласти рівняння (14.5) і розв’язати їх.

14. 4. Рух твердого тіла навколо нерухомої точки (сферичний рух)

Нехай тіло рухається так, що нерухомою залишається тільки одна його точка О. Такий рух тіла досить поширений у техніці (гіроскопи, бігунки, ротори, турбіни на кораблях, тощо). Пов’яжемо з тілом незмінні рухомі осі Ox, Oy, Oz. Як відомо, кінетичний момент механічної системи відносно нерухомої точки О визначається формулою:

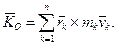(14.6)

Тверде тіло, що має одну нерухому точку О, в кожний даний момент часу обертається навколо миттєвої осі, що проходить через цю нерухому точку.

Швидкість k-тої точки такого тіла обчислюється за формулою:

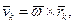(14.7)

де 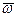- миттєва кутова швидкість тіла, 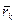- радіус-вектор k-тoї точки тіла, проведений з нерухомої точки О.

Підставимо значення 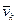з формули (14.7) в формулу (14.6) і одержимо кінетичний момент твердого тіла, що має одну нерухому точку О, відносно цієї точки:

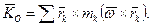(14.8)

При цьому проекції вектора 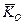на осі системи координат Oxyz, незмінно пов’язаної з тілом, дорівнюють:

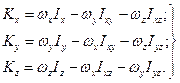(14.9)

Якщо за рухомі осі вибрати головні осі інерції тіла в точці О, то, як відомо, відцентрові моменти інерції дорівнюють нулю і кінетичні моменти відносно головних осей інерції визначаються за формулами:

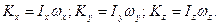(14.10)

В загальному випадку напрями векторів 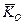і миттєвої кутової швидкості 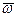між собою не співпадають.

В окремих випадках, коли еліпсоїд інерції тіла для точки О зводиться до кулі (І_x=І_y=І_z) або коли обертання тіла відбувається навколо однієї з головних осей інерції, наприклад осі z (ω_x=ω_y=0), напрями векторів кінетичного момента 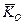і миттєвої кутової швидкості 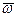між собою співпадають, тобто

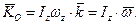
Кінетична енергія визначається так:

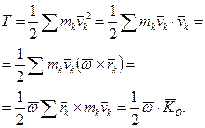(14.11)

Величина T>0, тому що кут між векторами 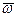і 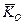буде завжди гострим.

З формул (14.10) і (14.11) одержимо:

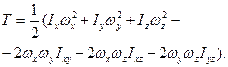(14.12)

Якщо за рухомі осі вибрати головні осі інерції в точці О, то

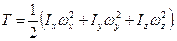(14.13)

Диференціальні рівняння руху твердого тіла можна одержати, використавши теорему про зміну кінетичного моменту, згідно якої

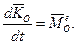(14.14)

Це рівняння описує рух тіла відносно нерухомої (інерціальної) системи координат Oxyz.

Похідна 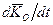визначає вектор абсолютної швидкості 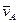точки А при русі її по годографу вектора 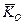(рис. 14.1), тобто

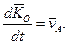
Тоді з рівняння (14.14) маємо:

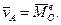(14.15)

Цей результат виражає теорему Резаля:

Рис. 14. 1.

абсолютна швидкість кінця вектора кінетичного моменту тіла, взятого відносно нерухомої точки, геометрично дорівнює головному моменту всіх діючих на тіло зовнішніх сил, взятому відносно тієї ж точки.

Рівняння (14.15) записують так:

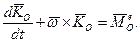(14.16)

Л.Ейлер запропонував проектувати рівняння (14.16) на рухомі осі Oxyz, незмінно пов’язані з рухомим тілом і направлені по головних осях інерції тіла в точці О. Опускаючи знак локальної похідної, маємо з рівняння (14.16):

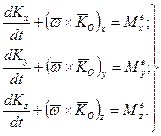(14.17)

Врахуємо, що

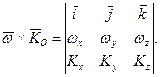
Тоді рівняння (14.17) можна записати у вигляді:

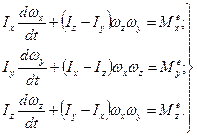(14.18)

Рівняння (14.18) були одержані Л.Ейлером і називаються динамічними рівняннями Ейлера.

Введемо позначення:

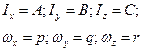
і до динамічних рівнянь Ейлера (14.18) приєднаємо кінетичні рівняння Ейлера. Одержимо шість нелінійних диференціальних рівнянь першого порядку відносно невідомих функції φ, ψ, θ (рис. 14.2):

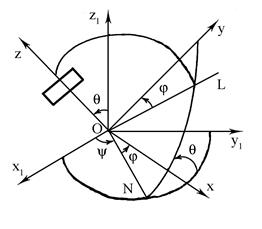
Рис. 14. 2.

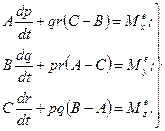(14.19)

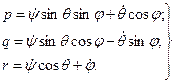(14.20)

Задачі динаміки для твердого тіла, що має одну нерухому точку, в змінних Ейлера φ (кут власного обертання), θ (кут нутації), ψ (кут прецесії) формулюються так:

1) знаючи закон руху тіла, який визначається рівняннями

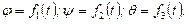(14.21)

знайти момент діючих на тіло сил;

2) знаючи момент діючих на тіло сил, знайти закон руху тіла у вигляді (14.21).

Розв’язання першої задачі динаміки зводиться до знаходження похідних від заданих функцій f₁(t), f₂(t), f₃(t), а розв’язання другої задачі динаміки зводиться до інтегрування системи диференціальних рівнянь (14.19) і (14.20). Інтегрування цієї системи рівнянь викликає значні математичні труднощі.

Зауваження. Для закріплення матеріалу §14 (пункти 14.1 – 14.4) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 37.12 – 37.16, 37.29, 39.2 – 39.7;

2) № 37.17 - 37.21, 37.24, 37.25, 37.27, 37.31, 37.34, 39.8, 39.11 - 39.15, 39.19;

3) № 37.22, 37.23, 37.33, 37.39, 37.40 – 37.42, 39.16 - 39.18, 39.20 – 39.22.

Рекомендується розв’язати також задачі № 10.2, 10.4, 10.5, 10.7, 10.14 – 10.18, 10.20, 10.23, 10.25, 10.26, 10.28 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Питання для самоконтролю

1. Запишіть диференціальне рівняння поступального руху твердого тіла.

2. Який висновок випливає з виду диференціального рівняння поступального руху твердого тіла?

3. Запишіть диференціальне рівняння обертального руху твердого тіла.

4. Сформулюйте план розв’язання задач динаміки обертального руху твердого тіла.

5. З яких рухів складається плоский рух твердого тіла?

6. Запишіть диференціальні рівняння плоского руху твердого тіла.

7. Яка послідовність розв’язування задач динаміки плоского руху твердого тіла?

8. Як визначаються вектор кінетичного моменту і його проекції на декартові осі координат та кінетична енергія тіла, яке виконує сферичний рух?

9. Виведіть диференціальне рівняння сферичного руху твердого тіла.

10. Запишіть і сформулюйте теорему Резаля.

11. Запишіть динамічні рівняння Ейлера.