В’язі. Класифікація в’язей

Будь-яку матеріальну точку M(x, y, z) називають вільною, якщо її можна перемістити, давши її координатам х, у, z малий приріст δх, δу, δz довільного знаку і величини. При цьому ніякі інші тіла не перешкоджають переміщенню точки М. Вільна матеріальна точка має три ступені вільності.

Матеріальну точку називають невільною, якщо її переміщення обмежене якимись умовами і їй не можна надати довільного руху. Обмеження, які накладаються на рух матеріальної точки, називають в’язями. В’язі завжди здійснюються іншими тілами і можуть обмежувати не тільки переміщення, але і швидкість та інші характеристики руху.

В’язі можуть бути накладені не тільки на матеріальні точки і на системи точок, але і на тверді тіла. Тверде тіло, рух якого не обмежений в’язями, називають вільним твердим тілом, а тверде тіло, рух якого обмежений в’язями, - невільним твердим тілом. Вільне тверде тіло має шість ступенів вільності.

В’язі називаються диференціальними, якщо їх рівняння утримують похідні координат або радіус - вектора за часом.

В’язі називаються геометричними, якщо їх рівняння не містять похідні координат за часом.

В’язі називаються стаціонарними, якщо їх рівняння не містять часу явно.

В’язі називаються нестаціонарними, якщо їх рівняння утримують явно час.

Двосторонні в’язі математично задаються рівняннями, односторонні - нерівностями.

Рівняння стаціонарних диференціальних двосторонніх в’язей має такий вигляд:

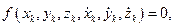k=1,2,..., n. (17.1)

Рівняння стаціонарних геометричних двосторонніх в’язей таке:

f(x_k, y_k, z_k)=0, k =1,2,...n. (17.2)

Неінтегровані диференціальні в’язі називаються неголономними.

Неінтегрованість полягає в тому, що ліву частину рівнянь в’язей не можна подати як повний диференціал якоїсь функції. В цьому випадку не можна шляхом інтегрування позбавитись від похідних від координат за часом в рівнянні в’язей.

Якщо в механічній системі є неголономна в’язь, то система називається неголономною.

Голономними в’язями називаються всі геометричні інтегровані диференціальні в’язі. Рівняння голономних в’язей або не мають похідних від координат, або їх можна привести до такого виду після інтегрування.

Загальне рівняння односторонніх в’язей має вигляд:

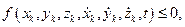k=1,2,…, n, (17.3)

де знак '=' відноситься до утримуючої в’язі, знак '<' відноситься до неутримуючої в’язі.

Приклад 1. Дві точки з’єднані жорстким стержнем довжини l. Рівняння в’язі

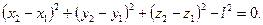
Приклад 2. Дві точки з’єднані ниткою довжини l. Рівняння в’язі

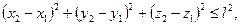
де '=' відноситься до натягнутої нитки, '<' відноситься до не натягнутої нитки. Ця в’язь одностороння геометрична і стаціонарна.

Приклад 3. Точка знаходиться на поверхні еліпсоїда, одна піввісь якого з часом видовжується. Рівняння в’язі

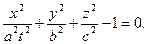
В’язь двостороння геометрична і нестаціонарна.

Питання для самоконтролю

1. Яка матеріальна точка називається вільною?

2. Скільки ступенів вільності має вільна матеріальна точка?

3. Яку матеріальну точку називають невільною?

4. Що називають в’язями?

5. Дайте визначення вільного і невільного твердого тіла.

6. Скільки ступенів вільності має вільне тверде тіло?

7. Які в’язі називають диференціальними?

8. Які в’язі є геометричними?

9. Дайте визначення стаціонарних і нестаціонарних в’язей.

10. Як відрізняються односторонні і двосторонні в’язі?

11. Запишіть загальний вигляд рівняння стаціонарної диференціальної двосторонньої в’язі.

12. Запишіть рівняння стаціонарної геометричної двосторонньої в’язі.

13. Які в’язі називають неголономними?

14. В чому полягає неінтегрованість в’язей?

15. Яка механічна система називається неголономною?

16. Які в’язі називають голономними?

17. Запишіть загальне рівняння односторонніх в’язей.