Можливі переміщення механічної системи

Можливим переміщенням механічної системи називається будь-яке уявне нескінченно мале переміщення її точок, що допускаються в даний момент часу накладеними на систему в’язями, або, іншими словами, всяке нескінченно мале переміщення точок системи, яке можуть здійснити ці точки в даний момент з данного їх положення без порушення в’язей.

Поняття можливого переміщення точок або механічної системи точок є, отже, поняттям чисто геометричним. Можливе переміщення точок системи не залежить від діючих на механічну систему сил, а залежить тільки від властивостей накладених на систему в’язей. При можливому переміщенні точок або системи накладені в’язі не зберігаються і не заважають цьому чисто геометричному переміщенню точки або системи. Переміщення, при яких дана точка або система залишає накладені в’язі, не будуть можливими.

Розглянемо, наприклад, матеріальну точку М, яка вимушена залишатись на нерухомій поверхні (рис. 17.1), заданій рівнянням

f(x, y, z) = 0, (17.4)

що є рівнянням утримуючої стаціонарної голономної в’язі. З рівняння (17.4) витікає, що дві з трьох координат точки М можна розглянути як незалежні змінні, які можуть приймати довільні значення, а третя координата визначається з рівняння в’язі. Точка М має два ступеня вільності. Візьмемо якесь положення точки М в довільний момент часу t (див. рис. 17.1) і уявимо собі, що хід часу зупинився і разом з ним зупинилась точка М в цьому положенні. Відволікаючись від дійсного руху точки і не враховуючи при цьому діючі на точку сили і вигляд її траєкторії, подивимось, по яких напрямах точці дозволяють переміщуватись з даного положення накладені на неї в’язі.

Рис. 17. 1.

В’язь - поверхня, тому вона дозволяє переміщуватись точці в будь - якому напрямі вздовж цієї поверхні. Вектор такого нескінченно малого переміщення точки М не сходить з даної поверхні і є

вектором можливого переміщення точки М, направленим по дотичній до поверхні в точці М в будь - який бік. Тобто, вектор можливого переміщення точки М лежить в дотичній площині. На рис. 17.1 вектор можливого переміщення позначено через 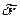, де 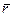- радіус - вектор точки М, проведений з початку координат. При русі точки М серед усіх її можливих переміщень є одне дійсне переміщення d 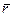, обумовлене не тільки характером накладеної в’язі, але і діючими на цю точку силами, а також початковими умовами.

В розглянутому випадку поверхня нерухома (в’язь стаціонарна), і траєкторія дійсного переміщення лежить на поверхні. В цьому випадку переміщення d 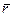направлене в бік руху точки по дотичній до траєкторії. Напрям вектора 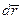співпадає з напрямом одного з можливих переміщень .

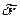Якщо поверхня рухається (в’язь нестаціонарна, f(x, y, z, t) = 0), то траєкторія дійсного руху уже не буде лежати на поверхні. Вектор d 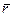, дотичний до траєкторії, в цьому випадку не буде лежати в дотичній до поверхні площині. Можливі переміщення 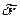визначаються при зупиненому часі, а значить, і при зупинених в’язях. Ось чому вектори 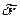залишаються, як і раніше, в дотичній до поверхні площині, і напрям вектора d 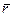в цьому випадку не співпадає ні з одним з напрямів .

Рис. 17. 2, а

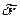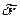Аналогічно для точки В (рис. 17.2, а) можливі переміщення будуть направлені

Рис. 17. 2, б

по осі х направо і наліво, дійсне переміщення d 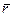також направлене по осі наліво. На схемі 17.2, б можливі переміщення 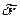залишаються паралельними до осі х, в той же час дійсне переміщення d 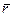направлене під деяким кутом до осі х за рахунок переміщення стола D у вертикальному напрямі. В цьому випадку під можливим переміщенням точки В необхідно розуміти її горизонтальне відносне переміщення

по відношенню до

Рис. 17. 2, а

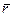рухомого стола. Вектор d описує абсолютне переміщення, яке складається з відносного переміщення і переносного переміщення разом зі столом у вертикальному напрямі.

З розглянутих прикладів можна зробити такі висновки:

1) у випадку стаціонарних голономних в’язей напрям дійсного переміщення d 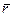точки співпадає з одним з її можливих переміщень ;

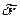2) у випадку нестаціонарних голономних в’язей дійсне переміщення d 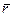точки в загальному випадку не співпадає з жодним з можливих переміщень .

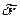Дійсне переміщення d 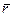є диференціалом функції 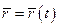, яка визначає закон руху точки. Можливе переміщення точки d 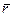за змістом є варіацією функції 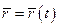. Варіацією функції називається елементарна зміна вигляду самої функції при незмінному значенні аргумента t.

Для вектора 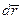маємо 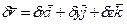, де величини 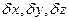називаються варіаціями координат х, у, z точки. Взяття варіацій функції виконується формально за тими ж правилами, що і диференціювання, якщо вважати, що 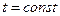. Взяттям варіацій рівнянь в’язей можна знайти залежність між варіаціями координат точки, на яку ця в’язь накладена.

Припустимо, що на матеріальну точку М з координатами х, у, z накладена стаціонарна голономна в’язь (17.4) і що ця точка одержала можливе переміщення, при якому її координати стали такими: 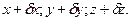Нові координати задовольняють рівнянням в’язі (17.4), тоді

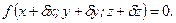
Розкладаємо ліву частину цього рівняння в ряд Тейлора з точністю до членів першого порядку:

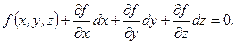
Але, згідно рівності (17.4) f(x, y, z) = 0 і, отже, будемо мати:

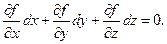(17.5)

Ліва частина рівняння (17.5) є повним диференціалом функції f(x, y, z)=0. Таким чином, при наявності стаціонарних в’язей виду f(x, у, z)=0 варіації 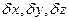координат х, у, z точки повинні задовольняти рівнянню (17.5). Користуючись поняттям градієнта від скалярної функції f(x, y, z)=0, рівняння (17.5) можна переписати так:

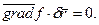(17.6)

Вектор 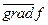направлений по зовнішній нормалі до поверхні f(x, y, z)=0, а тому рівняння (17.6) можна записати так:

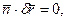(17.7)

де 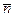- орт зовнішньої нормалі до поверхні f(x, y, z)=0. Рівняння (17.7) виражає умови перпендикулярності векторів 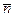і 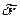. Це значить, що вектор можливого переміщення точки 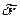лежить в площині, дотичній до поверхні f(x, y, z)=0.

Для дійсного переміщення точки М одержимо рівняння:

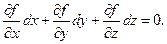
Порівнюючи цю рівність з (17.5), переконуємось, що у випадку стаціонарних в’язей проекції дійсного переміщення задовольняють тим же рівнянням, що і проекції можливого переміщення, або, що теж саме, дійсне переміщення є одним з можливих переміщень.

Припустимо тепер, що на матеріальну точку М накладена нестаціонарна голономна в’язь, що виражається рівнянням f(x, у, z, t)=0, а після можливого переміщення точки її координати стануть 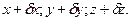Ці координати повинні задовольняти рівнянню в’язі, а, значить, при фіксованому часі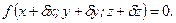

Розкладаючи ліву частину цього рівняння в ряд Тейлора і залишаючи члени першого порядку малості при справедливості рівняння f(x, у, z, t)=0, маємо:

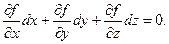(17.8)

Звідси видно, що нестаціонарність в’язі на варіації 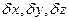ніякого впливу не здійснює.

У випадку нестаціонарної в’язі f(x, у, z, t)=0, виконуючи такі ж, як в попередньому випадку дії, одержимо:

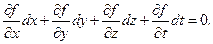(17.9)

Звідси

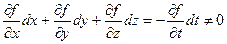
або 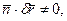тобто дійсне переміщення 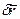точки не перпендикулярне з нормаллю до поверхні f(x, у, z, t)=0 в цій точці (не лежить в дотичній площині). Таким чином, якщо на точку накладена нестаціонарна в’язь f(x, у, z, t)=0, то дійсне переміщення 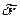матеріальної точки задовольняє вже іншому рівнянню, ніж можливе переміщення. Дійсне переміщення точки належить до ряду можливих переміщень тільки в тому випадку, коли в’язь, накладена на цю матеріальну точку, є стаціонарною; в цьому випадку 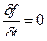і рівняння (17.9) співпадає з рівнянням (17.5).

Розглянемо механічну систему, що складається з n матеріальних точок, що мають 3n координат. Нехай на цю систему накладені h утримуючих стаціонарних голономних в’язей типу

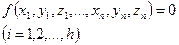(17.10)

Надамо системі деяке переміщення, внаслідок якого координати точок механічної системи одержать приріст 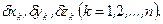Ці варіації, число яких дорівнює 3n, не будуть незалежними, бо внаслідок голономності в’язей (17.10) вони повинні задовольняти умовам виду

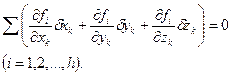(17.11)

Тільки (3n-h) варіацій є незалежними, що можуть одержати довільні значення, решта варіацій визначається з рівнянь (17.11).

Різниця між числом координат системи 3n і числом накладених на неї голономних в’язей, дорівнює числу ступенів вільності s цієї системи: s=3n-h. Отже, число ступенів вільності голономної системи дорівнює числу незалежних варіацій, тобто числу незалежних можливих переміщень, які може мати дана система.