Рассмотрим линейное неоднородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = f(x).

Общим решением этого уравнения на отрезке [a;b] называется функция y = Φ(x, C₁,..., C_n ), зависящая от n произвольных постоянных C₁,..., C_n и удовлетворяющая следующим условиям :

− при любых допустимых значениях постоянных C₁,..., C_n функция y = Φ(x, C₁,..., C_n ) является решением уравнения на [a; b] ;

− какова бы ни была начальная точка (x₀, y₀, y_1,0 ,..., y_{n − 1,0} ) , x₀∈ [a;b] , существуют такие значения C₁ =C₁₀ , ..., C_n = C_n0 , что функция y = Φ(x, C₁₀ , ..., C_n0) удовлетворяет начальным условиям y(x₀) = y₀, y '(x₀) = y_1,0 ,..., y^{(n − 1)} (x₀) = y_{n− 1,0} .

Справедливо следующее утверждение ( теорема о структуре общего решения линейного неоднородного уравнения).

Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b] , а функции y₁(x), y₂(x),..., y_n(x) образуют фундаментальную систему решений соответствующего однородного уравнения, то общее решение неоднородного уравнения имеет вид

y(x,C₁,..., C_n) = C₁ y₁(x) + C₂ y₂(x) + ... + C_n y_n(x) + y*(x),

где C₁,...,C_n — произвольные постоянные, y*(x) — частное решение неоднородного уравнения.

ВОПРОС 60. Фундаментальная система решений однородного линейного дифференциального уравнения. Свойства фундаментальной системы решений.

ВОПРОС 61. Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Построение общего решения однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами.

Однородное уравнение второго порядка:

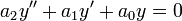
интегрируется следующим образом:

Пусть 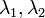— корни характеристического уравнения.

,

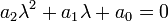являющегося квадратным уравнением.

Вид общего решения однородного уравнения зависит от значения дискриминанта :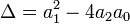

• при 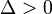уравнение имеет два различных вещественных корня

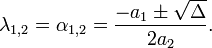
Общее решение имеет вид: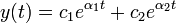

• при 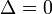— два совпадающих вещественных корня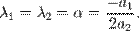

Общее решение имеет вид: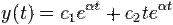

• при 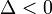существуют два комплексно сопряженных корня

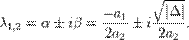
Общее решение имеет вид:

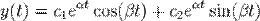
ВОПРОС 62. Линейное дифференциальное уравнение второго порядка с правой частью стандартного вида. Построение частного решения по виду правой части.