Метод вариации произвольных постоянных для построения решений системы линейных дифференциальных уравнений в векторной нормальной форме
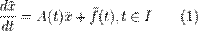
состоит в построении частного решения (1) в виде
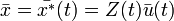
где 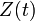 — базис решений соответствующего однородного уравнения, записанный в виде матрицы, а векторная функция
— базис решений соответствующего однородного уравнения, записанный в виде матрицы, а векторная функция 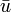 , заменившая вектор произвольных постоянных, определена соотношением
, заменившая вектор произвольных постоянных, определена соотношением 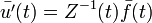 . Искомое частное решение (с нулевыми начальными значениями при
. Искомое частное решение (с нулевыми начальными значениями при 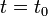 имеет вид
имеет вид
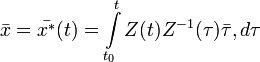
Для системы с постоянными коэффициентами последнее выражение упрощается:
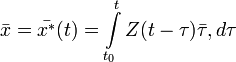
Матрица 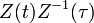 называется матрицей Коши оператора
называется матрицей Коши оператора 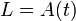 .
.
ВОПРОС 64. Приложения методов теории дифференциальных уравнений в моделировании таможенных процессов.
ВОПРОС 65. Пространство элементарных событий. Алгебра событий. Частота случайного события. Свойства частот.
ВОПРОС 66. Вероятность события. Классическая вероятность. Свойства вероятности
ВОПРОС 67. Комбинаторика. Применение комбинаторных схем при вычислении вероятностей сложных событий.
Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике).
ВОПРОС 68. Полная группа несовместных событий. Свойства вероятностей для полной группы событий.
несовместными – события А1 – А6
Из определения несовместных событий следует, что их произведение является невозможным событием
Соб. Н1, Н2…Нn в некоем опыте G образ.полную группу несовмест.событий, если они попарно несовместны и в рез-те опыта произойдет хотя бы одно из событий Нi.
Н1+Н2+…+Нn =Ω
При этом соб. Н1, Н2…Нn , к-рыеимеютположит.вер-ть, нзв гипотезами.
Если соб. Н1, Н2…Нnобраз.полную группу, то
Р(Н1)+Р(Н2)+…+Р(Нn) =Р(Н1+Н2+…+Нn)=1
Для любого соб.А вер-ть противоположного соб.Ā определяется по формуле: Р(Ā)=1-Р(А)
Док-во: Ā= Ω/А, А*Ā= Ø — несовмест., А+Ā= Ω
Р(А+Ā)=1; по аскиоме 3: Р(А+Ā)=Р(А)+Р(Ā)=1
=>Р(Ā)=1- Р(А)
ВОПРОС 69. Теоремы сложения и умножения вероятностей. Независимость и несовместность событий.
Суммой двух событий А и В называется событие С, состоящее в появлении хотя бы одного из событий А или В.
Теорема сложения вероятностей
Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:
Р (А + В) = Р (А) + Р (В).
В случае, когда события А и В совместны, вер-ть их суммы выражается формулой
Р (А +В) = Р (А) + Р (В) – Р (АВ),
где АВ – произведение событий А и В.
Два события называются зависимыми, если вероятность одного из них зависит от наступления или не наступления другого.в случае зависимых событий вводится понятие условной вероятности события.
Условной вероятностью Р(А/В) события А называется вероятность события А, вычисленная при условии, что событие В произошло. Аналогично через Р(В/А) обозначается условная вероятность события В при условии, что событие А наступило.
Произведением двух событий А и В называется событие С, состоящее в совместном появлении события А и события В.
Теорема умножения вероятностей
Вероятность произведения двух событий равна вер-ти одного из них, умноженной на условную вероятность другого при наличии первого:
Р (АВ) = Р(А) · Р(В/А), или Р (АВ) = Р(В) · Р(А/В).
Следствие. Вероятность совместного наступления двух независимых событий А и В равна произведению вероятностей этих событий:
Р (АВ) = Р(А) · Р(В).
Следствие. При производимых n одинаковых независимых испытаниях, в каждом из которых события А появляется с вероятностью р, вероятность появления события А хотя бы один раз равна 1 - (1 - р)n
ВОПРОС 70. Формула полной вероятности. Формула Байеса.
Если событие А может произойти только при выполнении одного из событий 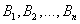 , которые образуют полную группу несовместных событий, то вероятность события Авычисляется по формуле
, которые образуют полную группу несовместных событий, то вероятность события Авычисляется по формуле
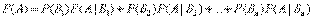 .
.
Эта формула называется формулой полной вероятности.
Вновь рассмотрим полную группу несовместных событий 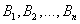 , вероятности появления которых
, вероятности появления которых 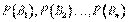 . Событие А может произойти только вместе с каким-либо из событий
. Событие А может произойти только вместе с каким-либо из событий 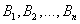 , которые будем называть гипотезами. Тогда по формуле полной вероятности
, которые будем называть гипотезами. Тогда по формуле полной вероятности
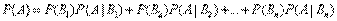
Если событие А произошло, то это может изменить вероятности гипотез 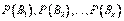 .
.
По теореме умножения вероятностей
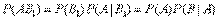 ,
,
откуда
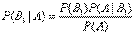 .
.
Аналогично, для остальных гипотез
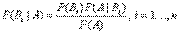
Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез 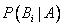 называются апостериорными вероятностями, тогда как
называются апостериорными вероятностями, тогда как 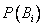 -априорными вероятностями.
-априорными вероятностями.
Пример. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.
Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через 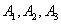 обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.
обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.
Можно применить формулу полной вероятности, причем в наших обозначениях:
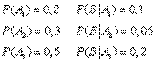
Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:
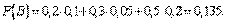
Пример. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.
Решение. Возможны три гипотезы: 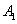 - на линию огня вызван первый стрелок,
- на линию огня вызван первый стрелок, 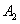 - на линию огня вызван второй стрелок,
- на линию огня вызван второй стрелок, 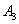 - на линию огня вызван третий стрелок.
- на линию огня вызван третий стрелок.
Так как вызов на линию огня любого стрелка равновозможен, то 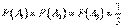
В результате опыта наблюдалось событие В - после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:
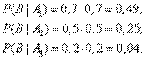
по формуле Байеса находим вероятность гипотезы 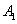 после опыта:
после опыта:
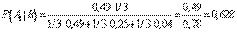
Пример. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго.
а) Каков процент брака на конвейере?
б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере?
Решение. Возьмем с конвейера наудачу одну деталь и рассмотрим событие А – деталь бракованная. Оно связано с гипотезами относительно того, где была обработана эта деталь: 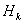 – взятая наудачу деталь обработана на
– взятая наудачу деталь обработана на 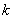 -ом станке,
-ом станке, 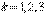 .
.
Условные вероятности (в условии задачи они даны в форме процентов):
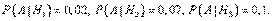
Зависимости между производительностями станков означают следующее:
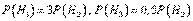 .
.
А так как гипотезы образуют полную группу, то 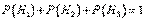 .
.
Решив полученную систему уравнений, найдем: 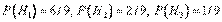 .
.
а) Полная вероятность того, что взятая наудачу с конвейера деталь – бракованная:
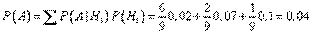 .
.
Другими словами, в массе деталей, сходящих с конвейера, брак составляет 4%.
б) Пусть известно, что взятая наудачу деталь – бракованная. Пользуясь формулой Байеса, найдем условные вероятности гипотез:
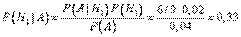 ,
,
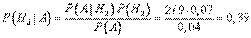 ,
,
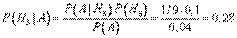 .
.
Таким образом, в общей массе бракованных деталей на конвейере доля первого станка составляет 33%, второго – 39%, третьего – 28%.
ВОПРОС 71.Повторение опытов. Формула Бернулли. Полиномиальные вероятности.
При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.
Примеры повторных испытаний:
1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;
2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А в единичном испытании буквой р, т.е. 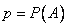 , а вероятность противоположного события (событие А не наступило) - буквой
, а вероятность противоположного события (событие А не наступило) - буквой 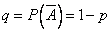 .
.
Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли

Распределение числа успехов (появлений события) носит название биномиального распределения.
Пример. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
Решение. Событие А – достали белый шар. Тогда вероятности
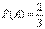 ,
, 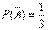 .
.
По формуле Бернулли требуемая вероятность равна
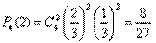 .
.
Пример. Определить вероятность того, что в семье, имеющей 5 детей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
Решение. Вероятность рождения девочки
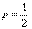 , тогда
, тогда 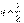 .
.
Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:
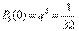 ,
, 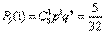 ,
,
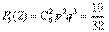 ,
, 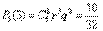 .
.
Следовательно, искомая вероятность
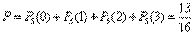 .
.
Пример. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.
Решение. Здесь опыт заключается в проверке каждой из 30 деталей на качество. Событие А - «появление нестандартной детали», его вероятность 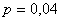 , тогда
, тогда 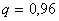 . Отсюда по формуле Бернулли находим
. Отсюда по формуле Бернулли находим
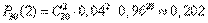 .
.
Пример. При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.
Решение. Вычисляем по формуле Бернулли:
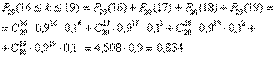
Пример. Независимые испытания продолжаются до тех пор, пока событие А не произойдет k раз. Найти вероятность того, что потребуется n испытаний (n ³ k), если в каждом из них 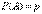 .
.
Решение. Событие В – ровно n испытаний до k-го появления события А – есть произведение двух следующий событий:
D – в n-ом испытании А произошло;
С – в первых (n–1)-ом испытаниях А появилось (к-1) раз.
Теорема умножения и формула Бернулли дают требуемую вероятность:
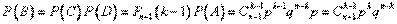
Надо заметить, что использование биномиального закона зачастую связано с вычислительными трудностями. Поэтому с возрастанием значений n и m становится целесообразным применение приближенных формул (Пуассона, Муавра-Лапласа), которые будут рассмотрены в следующих разделах.
ВОПРОС 72.Случайные величины. Дискретные и непрерывные случайные величины. Числовые характеристики случайных величин.
Дата добавления: 2016-07-18; просмотров: 2451;











