Распределение Пуассона

Пусть имеется некоторая последовательность событий, наступающих в случайные моменты времени (будем называть это потоком событий). Интенсивность потока (среднее число событий, появляющихся в единицу времени) равна λ. Пусть этот поток событий - простейший (пуассоновский), т.е. обладает тремя свойствами:
1) вероятность появления k событий за определённый промежуток времени зависит только от длины этого промежутка, но не от точки отсчёта, другими словами, интенсивность потока есть постоянная величина (свойство стационарности);
2) вероятность появления k событий в любом промежутке времени не зависит от того, появлялись события в прошлом или нет (свойство «отсутствия последействия»);
3) появление более одного события за малый промежуток времени практически невозможно (свойствоординарности).
Вероятность того, что за промежуток времени t событие произойдёт k раз, равна

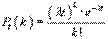
4. Непрерывная случайная величина,
интегральная и дифференциальная функции распределения.

Непрерывной называют случайную величину, которая может принимать любые значения из некоторого заданного интервала, например, время ожидания транспорта, температура воздуха в каком-либо месяце, отклонение фактического размера детали от номинального, и т.д. Интервал, на котором она задана, может быть бесконечным в одну или обе стороны.

Плотность вероятности непрерывной случайной величины, она же дифференциальная функция распределения вероятностей - аналог закона распределения дискретной с.в. Но если закон распределения дискретной с.в. графически изображается в виде точек, соединённых для наглядности ломаной линией (многоугольник распределения), то плотность вероятностей графически представляет собой непрерывную гладкую линию (или кусочно-гладкую, если на разных отрезках задаётся разными функциями). Аналитически задаётся формулой.
Если закон распределения дискретнойс.в. ставит каждому значению x в соответствие определённую вероятность, то про плотность распределения такого сказать нельзя. Для непрерывныхс.в. можно найти только вероятность попадания в какой-либо интервал. Считается, что для каждого отдельного (одиночного) значения непрерывной с.в. вероятность равна нулю. И графически вероятность попадания в интервал выражается площадью фигуры, ограниченной сверху графиком плотности вероятности, снизу осью ОХ, с боков - рассматриваемым интервалом.
Свойства плотности вероятности:
1) Значения функции неотрицательны, т.е. f(x)≥0
2) Основное свойство плотности вероятности: несобственный интеграл от плотности вероятности в пределах от -∞ до +∞ равен единице (геометрически это выражается тем, что площадь фигуры, ограниченной сверху графиком плотности вероятности, снизу - осью OX, равна 1).

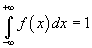
Функция распределения случайной величины, она же интегральная функция распределения вероятностей - это функция, определяющая для каждого значения x вероятность того, что случайная величина (ξ) примет значение меньшее, чем x: F(x) = P(ξ < x). Численно функция распределения равна площади фигуры, ограниченной сверху графиком плотности вероятности, снизу осью ОХ, с боков - рассматриваемым интервалом.
Основные свойства:
1) Значения функции распределения лежат в интервале [0; 1], т.е. 0 ≤ F(X) ≤ 1
2) Это функция неубывающая, при x→-∞ F(X)→0, при x→+∞ F(X)→1
3) Вероятность попадания в интервал (a, b) определяется формулой F(b) - F(a)

Взаимосвязь интегральной и дифференциальной функций распределения вероятностей: