Числовые характеристики непрерывных случайных величин

Математическое ожидание непрерывной случайной величины вычисляется по формуле:

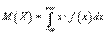
В частности, если с.в. задана своей плотностью вероятности на каком-либо отрезке, то и интеграл вычисляем на этом отрезке.

Дисперсия непрерывной случайной величины вычисляется по формуле:

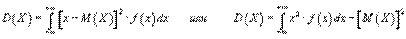
Относительно пределов интегрирования - то же самое.

Среднее квадратическое отклонение непрерывной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии:
σ(X) = √D(X)

Мода непрерывной случайной величины Mo(X) - значение с.в., имеющее наибольшую вероятность. Если в задаче требуется определить моду - находим экстремум (максимум) плотности вероятности f(x).

Коэффициент вариации непрерывной случайной величины вычисляется по той же формуле, что и для дискретной с.в.:
V(X) = |σ(X)/M(X)| · 100%

Асимметрия (коэффициент асимметрии) случайной величины As(X) - величина, характеризующая степень асимметрии распределения относительно математического ожидания. Коэффициент асимметрии непрерывной случайной величины вычисляется по формуле:

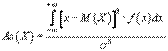
Если коэффициент асимметрии отрицателен, то либо большая часть значений случайной величины, либо мода находятся левее математического ожидания, и наоборот, если As(X)>0, то правее.

Эксцесс (коэффициент эксцесса) случайной величины Ex(X) - величина, характеризующая степень островершинности или плосковершинности распределения. Коэффициент эксцесса непрерывной случайной величины вычисляется по формуле:

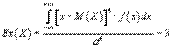
Распределений