I.1.5 РАВНОПЕРЕМЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ

Равнопеременное прямолинейное движение является частным случаем неравномерного движения, ускорение при котором остаётся постоянным как по модулю, так и по направлению ( .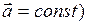

Среднее ускорение 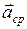будет равно мгновенному ускорению . Направлено ускорение вдоль траектории точки. Нормальное ускорение при этом отсутствует .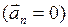

Если направление ускорения совпадает с направлением скорости 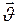то, движение называется равноускоренным. Модуль скорости равноускоренного движения точки с течением времени возрастает.

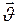Если направление векторов ускорения и скорости противоположны то, движение называется равнозамедленным. Модуль скорости при равнозамедленном движении точки с течением времени уменьшается.

Изменение скорости 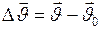в течение промежутка времени 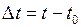при равнопеременном прямолинейном движении равно: 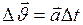, или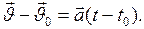

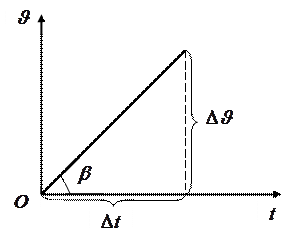
На графике это можно будет представить следующим образом (рис.11).

	Рисунок 11 – График зависимости скорости от времени

На данном графике ускорение характеризуется тангенсом угла между касательной к скорости и осью времени: .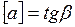

Если в начальный момент времени 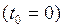скорость точки равна 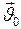(начальная скорость) и ускорение известно, то скорость 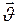в произвольный момент времени :

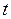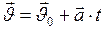. (I.13)

Проекция вектора скорости на ось прямоугольной декартовой системы координат связана с соответствующими проекциями векторов начальной скорости и ускорения уравнением:

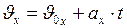. (I.13^/)

Аналогично записываются уравнения для проекций вектора скорости на другие координатные оси.

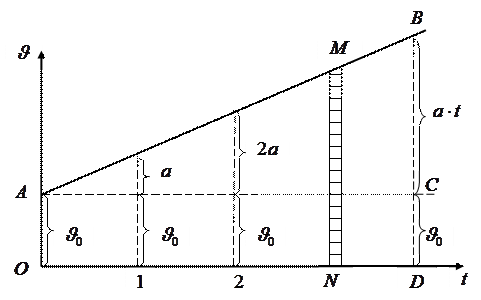
Формулы (I.13) и (I.13^/) выражают алгебраическую зависимость скорости от времени и представляют собой первый закон равнопеременного движения. Та же зависимость может быть наглядно представлена графически (рис.12). Будем откладывать на оси абсцисс время 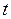, а на оси ординат скорость 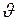в соответствующие моменты времени; к первоначальной скорости 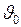каждую секунду, прибавляется приращение .

	Рисунок 12 – Графическое представление первого закона равнопеременного движения

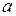Второй закон равнопеременного движения - устанавливает связь между пройденным расстоянием и временем движения (т.е. даёт уравнение этого движения). Получим его графическим методом, используя рисунок 12. Для этого разобьём площадь 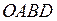на узкие полоски 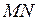и примем площадь каждой из них за площадь прямоугольника; она и выразит путь, пройденный материальной точкой за малый промежуток времени , в течение которого скорость можем принимать постоянной. Составив сумму таких площадей, определим путь, пройденный за время движения 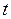. Но сумма этих площадей и будет как раз площадью 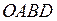. Поэтому, выразив эту площадь в функции времени, мы и найдём зависимость от :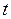

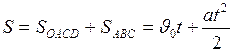. Эта формула устанавливает искомую зависимость пройденного при равнопеременном движении расстояния от времени (второй закон равнопеременного движения):

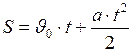. (I.14)

При 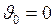путь равен:

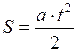. (I.15)

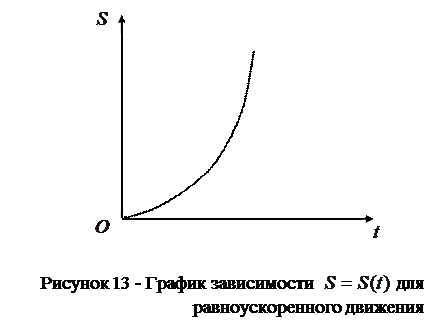
График зависимости 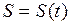для равноускоренного движения изображён на рисунке 13.

При прямолинейном равнозамедленном движении формула пути:

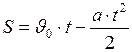. (I.16)

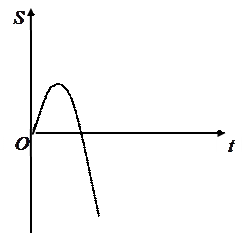График зависимости 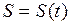для равнозамедленного движения изображён на рисунке 14.

	Рисунок 14 - График зависимости для равнозамедленного движения

Окончательно два закона равнопеременного движения будут выглядеть следующим образом:

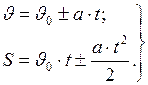(I.17)

Из этих двух законов вытекают некоторые соотношения, имеющие частое применение в задачах и технике.

1. Для равноускоренного движения без начальной скорости (как уже говорилось выше) эти законы упрощаются:

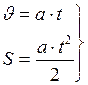(I.18)

2. Исключая время 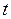, получаем формулу для нахождения скорости 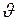в конце пройденного пути :

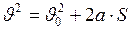. (I.19)

при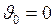

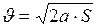. (I.20)

3. Обозначим через 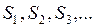расстояния, проходимые в одну, две, три,…секунды; имеем:

; ; ; ;…;

; ; ;…;

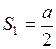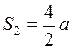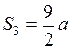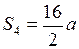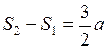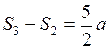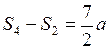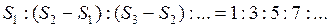
Расстояния, проходимые в последовательные единицы времени, относятся, как ряд нечётных чисел.

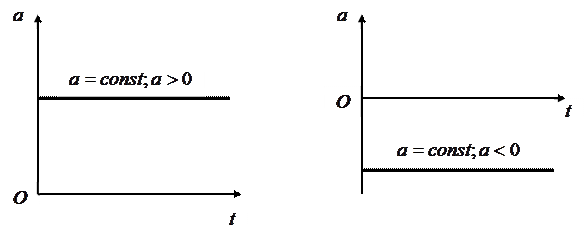
Осталось рассмотреть графики зависимости ускорения от времени при равноускоренном и равнозамедленном движениях.

График 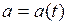при равноускоренном движении представляет собой линию, параллельную оси времени и расположенную выше этой оси (рис.15,а).

График 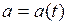при равнозамедленном движении представляет собой линию, параллельную оси времени и расположенную ниже этой оси (рис.15,б).

а)

б)

	Рисунок 15 – Графики зависимостей : а) при равноускоренном и б) при равнозамедленном движениях.