Равномерное распределение

Плотность вероятности равномерного распределения сохраняет на интервале (a, b) постоянное значение, вне этого интервала плотность вероятности равна нулю. Исходя из основного свойства плотности вероятности,
f(x) = 1/(b-a) на интервале (a;b).
Интегральную функцию распределения (вероятность того, что с.в. примет значение меньшее, чем x) находим как интеграл от -∞ до x от плотности вероятности: F(x) = (x-a)/(b-a)
Графики плотности вероятности и функции равномерного распределения:

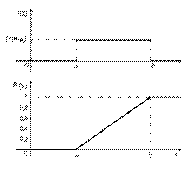
Математическое ожидание равномерного распределения: M(X) = (a + b)/2
Дисперсия равномерного распределения: D(X) = (b - a)²/12
Среднее квадратичное отклонение равномерного распределения: σ(X) = (b - a)/(2√3)

ВОПРОС 73. Функция распределения. Ряд распределения дискретной случайной величины, плотность вероятности непрерывной случайной величины.

ВОПРОС 74. Корреляционная зависимость между двумя случайными величинами.

ВОПРОС 75. Приложения методов теории вероятностей в моделировании таможенных процессов.

ВОПРОС 76. Сущность выборочного метода. Вариационный ряд. Выборочная функция распределения. Полигон частот и гистограмма.

ВОПРОС 77. Выборочные моменты. Точечное и интервальное оценивание параметров распределений.

ВОПРОС 78. Основные распределения статистики: распределение χ – квадрат, распределение Стьюдента, распределение Фишера.

ВОПРОС 79. Проверка простой статистической гипотезы против простой альтернативы. Постановка задачи, основные виды критических областей.

Проверка статистических гипотез – это один из основных методов математической статистики, который используется в эконометрике.

С помощью методов математической статистики можно проверить предположения о законе распределения некоторой случайной величины (генеральной совокупности), о значениях параметров этого закона (например, математического ожидания или дисперсии), о наличии корреляционной зависимости между случайными величинами, определенными на множестве объектов одной и той же генеральной совокупности.

Статистической гипотезой называется любое предположение о виде неизвестного закона распределения или о параметрах известных распределений.

Проверка статистической гипотезы означает проверку соответствия выборочных данных выдвинутой гипотезе.

Параллельно с выдвигаемой основной гипотезой рассматривают и противоречащую ей гипотезу, которая называется конкурирующей или альтернативной. Противоречащая гипотеза считается справедливой, если основная выдвинутая гипотеза отвергается.

Нулевой, основной или проверяемой гипотезой называется первоначально выдвинутая гипотеза, которая обозначается Н0.

Конкурирующей или альтернативной гипотезой называется гипотеза, которая противоречит основной гипотезе Н0 и обозначается Н1.

Например, основная гипотеза Н0 состоит в том, что математическое ожидание μ равно значению μ0. В этом случае конкурирующая гипотеза Н1 может состоять в предположении, что математическое ожидание μ не равно (больше или меньше) значения μ0: Н0: μ=μ0; Н1: μ≠μ0, или Н1: μ>μ0, или Н1: μ<μ0.

Проверка статистической гипотезы означает проверку согласования исходных выборочных данных с выдвинутой основной гипотезой. При этом возможно возникновение двух ситуаций – основная гипотеза может подтвердиться, а может и опровергнуться. Следовательно, при проверке статистических гипотез существует вероятность допустить ошибку, приняв или опровергнув верную гипотезу.

При проверке статистических гипотез можно допустить ошибки первого или второго рода

Ошибкой первого рода называется ошибка, состоящая в опровержении верной гипотезы.

Ошибкой второго рода называется ошибка, состоящая в принятии ложной гипотезы.

Уровнем значимостиа называется вероятность совершения ошибки первого рода.

Значение уровеня значимости а обычно задаётся близким к нулю (например, 0,05; 0,01;0,02 и т. д.), потому что чем меньше значение уровеня значимости, тем меньше вероятность совершения ошибки первого рода, состоящую в опровержении верной гипотезы Н0.

Проверка справедливости сттатистическвх гипотез осуществляется с помощью различных статистических критериев.

Статистическим критерием называется случайная величина, которая используется с целью проверки нулевой гипотезы.

Статистические критерии называются соответственно тому закону распределения, которому они подчиняются, т. е. F-критерий подчиняется распределению Фишера-Снедекора, χ2-критерий подчиняется χ2-распределению, Т-критерий подчиняется распределению Стьюдента, U-критерий подчиняется нормальному распределению.

Наблюдаемым значением статистического критерия называется значение критерия, которое рассчитано по выборочной совокупности, подчиняющейся определённому закону распределения.

Множество всех возможных значений выбранного статистического критерия делится на два непересекающихся подмножества. Первое подмножество включает в себя те значения критерия, при которых основная гипотеза отвергается, а второе подмножество – те значения критерия, при которых основная гипотеза принимается.

Критической областью называется множество возможных значений статистического критерия, при которых основная гипотеза отвергается.

Областью принятия гипотезы или областью допустимых значений называется множество возможных значений статистического критерия, при которых основная гипотеза принимается.

Если наблюдаемое значение статистического критерия, рассчитанное по данным выборочной совокупности, принадлежит критической области, то основная гипотеза отвергается. Если наблюдаемое значение статистического критерия принадлежит области принятия гипотезы, то основная гипотеза принимается.

Критическими точками или квантилями называются точки, разграничивающие критическую область и область принятия гипотезы.

Критические области могут быть как односторонними, так и двусторонними.

При проверке статистических гипотез используют правосторонние, левосторонние и двусторонние критические области.

Правосторонняя критическая область характеризуется неравенством вида: L>lкр,

где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;

lкр, – это положительное значение статистического критерия, определяемое по таблице распределения данного критерия.

Следовательно, для определения правосторонней критической области необходимо рассчитать положительное значение статистического критерия lкр.

Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, вероятность того, что значение статистического критерия L будет больше значения lкр, равна заданному уровню значимости, т.е. P(L>lкр)=a.

Для каждого статистического критерия рассчитаны специальные таблицы, с помощью которых определяют критическую точку, удовлетворяющую заданному уровню значимости.

Левосторонняя критическая область характеризуется неравенством вида: L<lкр,

где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;

lкр, — это отрицательное значение статистического критерия, определяемое по таблице распределения данного критерия.

Следовательно, для определения левосторонней критической области необходимо найти рассчитать отрицательное значение статистического критерия lкр.

Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, вероятность того, что значение статистического критерия L будет меньше значения lкр, равна заданному уровню значимости, т.е. P(L<lкр)=a.

Двусторонняя критическая область характеризуется двумя неравенствами вида: L>lкр1 и L<lкр2,

где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;

lкр1 – это положительное значение статистического критерия, определяемое по таблице распределения данного критерия; lкр2 — это отрицательное значение статистического критерия, определяемое по таблице распределения данного критерия; lкр1> lкр2.

Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, сумма вероятностей того, что значение статистического критерия L будет больше значения lкр1 или меньше значения lкр2, равна заданному уровню значимости, т.е. P(L>lкр1)+(L<lкр2)=a.

Выбор критической области осуществляется исходя из вида конкурирующей гипотезы Н1. При этом применяются следующие правила:

1) правосторонняя критическая область выбирается в том случае, если Н1:>;

2) левосторонняя критическая область выбирается в том случае, если Н1:‹;

3) двусторонняя критическая область выбирается в том случае, если Н1:≠.

Предположим, что заданы следующие параметры:

1) статистический критерий L;

2) критическая область W, где H0 отклоняется;

3) область принятия гипотезы где H0 не отклоняется;

4) вероятность совершить ошибку первого рода a;

5) вероятность совершить ошибку второго рода β.

Тогда справедливо утверждение о том, что выражение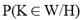

является вероятностью того, что статистический критерий L попадёт в критическую область, если верна гипотеза H.

При построении критической области учитываются два требования:

1) вероятность того, что статистический критерий L попадёт в критическую область, если верна Н0, равна а: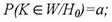

данное равенство задаёт вероятность совершения ошибки первого рода;

2) вероятность того, что статистический критерий L попадёт в критическую область (область отклонения гипотезы Н0 в пользу гипотезы Н1), если верна гипотеза Н1: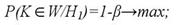

данное равенство задаёт вероятность принятия правильной гипотезы.

ВОПРОС 80.Линейная регрессия. Определение параметров регрессионного уравнения методом наименьших квадратов.

Линейная регрессия — метод восстановления зависимости между двумя переменными. Ниже приведен пример программы, которая строит линейную модель зависимости по заданной выборке и показывает результат на графике.

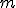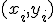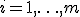Для заданного множества из пар , , значений свободной и зависимой переменной требуется построить зависимость. Назначена линейная модель

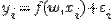
c аддитивной случайной величиной . Переменные 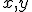принимают значения на числовой прямой 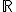. Предполагается, что случайная величинараспределена нормально с нулевым матожиданием и фиксированной дисперсией 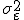, которая не зависит от переменных 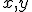. При таких предположениях параметры 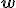регрессионной модели вычисляются с помощью метода наименьших квадратов.

Метод наименьших квадратов (МНК, OLS, Ordinary Least Squares) — один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.

Необходимо отметить, что собственно методом наименьших квадратов можно назвать метод решения задачи в любой области, если решение заключается или удовлетворяет некоторому критерию минимизации суммы квадратов некоторых функций от искомых переменных. Поэтому метод наименьших квадратов может применяться также для приближённого представления (аппроксимации) заданной функции другими (более простыми) функциями, при нахождении совокупности величин, удовлетворяющих уравнениям или ограничениям, количество которых превышает количество этих величин и т.д.

Пусть задана некоторая (параметрическая) модель вероятностной (регрессионной) зависимости между (объясняемой) переменной y и множеством факторов (объясняющих переменных) x

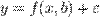Где 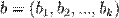- вектор неизвестных параметров модели

- случайная ошибка модели.

Пусть также имеются выборочные наблюдения значений указанных переменных. Пусть 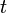- номер наблюдения ( 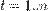). Тогда 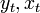- значения переменных в 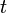-м наблюдении. Тогда при заданных значениях параметров b можно рассчитать теоретические (модельные) значения объясняемой переменной y: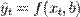

Тогда можно рассчитать остатки регрессионной модели - разницу между наблюдаемыми значениями объясняемой переменной и теоретическими (модельными, оцененными):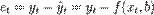

Величина остатков зависит от значений параметров b.

Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры b, при которых сумма квадратов остатков будет минимальной:

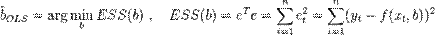
В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS - англ. Non-Linear Least Squares). Во многих случаях возможно аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции ESS(b) - продифференцировать функцию 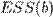по неизвестным параметрам b, приравнять производные к нулю и решить полученную систему уравнений:

Если случайные ошибки модели имеют нормальное распределение, имеют одинаковую дисперсию и некоррелированы между собой, МНК-оценки параметров совпадают с оценкамиметода максимального правдоподобия (ММП).