Нормальное распределение

Нормальное распределение имеет плотность вероятности 1/[σ√2π]·e^-(x-a)2/2σ2, где a - математическое ожидание, σ - среднее квадратическое отклонение.

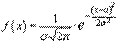
Значения плотности нормального распределения для конкретного числового значения x можно вычислить в Excel с помощью формулы =НОРМРАСП(x;a;σ;0). Если a = 0, σ = 1, то такое нормальное распределение называется стандартным. Значения плотности стандартного нормального распределения можно посмотреть в таблице или вычислить в Excel с помощью формулы =НОРМРАСП(x;0; 1;0)
График нормального распределения имеет куполообразную форму, он симметричен относительно своего математического ожидания, а на степень его островершинности влияет величина среднего квадратичного отклонения σ.

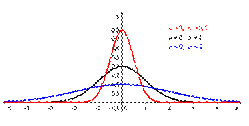
Асимметрия, эксцесс, мода и медиана нормального распределения равны:
As(X) = 0; Ex(X) = 0; Mo(X) = a; Me(X) = a, где а - математическое ожидание.

Интегральная функция нормального распределения вероятностей:

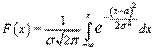
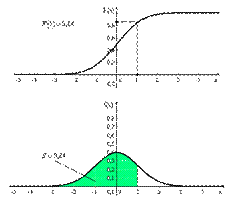
Интегральная функция распределения вероятностей показывает вероятность того, что с.в. примет значение меньшее, чем x: F(x) = P(ξ < x). Численно она равна площади криволинейной трапеции, ограниченной сверху графиком плотности вероятности, снизу осью OX, на интервале от -∞ до x. Ниже дана иллюстрация.