IV. Дифференциальное исчисление
Определение производной
Производная 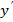 или f’(x) от данной функции y=f(x) есть предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю:
или f’(x) от данной функции y=f(x) есть предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю:
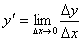 или
или 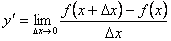 .
.
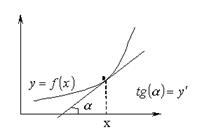
Механический смысл производной – скорость изменения функции. Геометрический смысл производной – тангенс угла наклона касательной к графику функции:
Основные правила дифференцирования
| Наименование | Функция | Производная |
| Умножение на постоянный множитель | cy | cy’ |
| Алгебраическая сумма двух функций | u+v | u’+v+ |
| Произведение двух функций | uv | u’v+uv’ |
| Частное двух функций | 
| 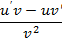
|
| Сложная функция | y=f(u)
u= 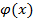
| y’= 
|
Производные основных элементарных функций
| № п/п | Наименование функции | Функция и её производная |
| Константа С | С’=0 | |
| Степенная функция Частные случаи | 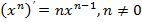
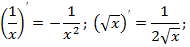
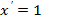
| |
| Показательная функция Частный случай | 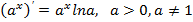
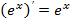
| |
| Логарифмическая функция Частный случай | 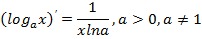
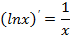
| |
| Тригонометрические функции | 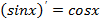

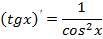
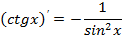
| |
| Обратные тригонометрические функции | 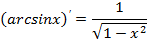
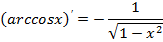
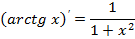
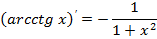
|
Пример 17
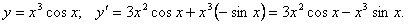

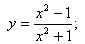
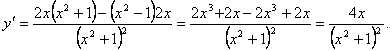
Дата добавления: 2016-06-05; просмотров: 2280;











