Уравнение неразрывности.

Применяя закон сохранения массы к жидкости, протекающей через фиксированный объем, получим уравнение неразрывности:

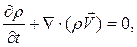(2.1.1)

где 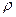– плотность жидкости, а 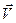– ее скорость. Слагаемые (2.1.1) имеют следующий физический смысл: первый член уравнения дает увеличение плотности в контрольном объеме за единицу времени; второй – поток массы через поверхность контрольного объема за единицу времени, отнесенный к единице объема. Удобно воспользоваться понятием субстанциональной производной:

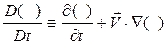, (2.1.2)

для преобразования уравнения (2.1.1) к виду

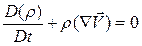. (2.1.3)

Уравнение (2.1.1) было выведено с использованием подхода Эйлера. В этом подходе фиксируется контрольный объем и рассматривается баланс жидкости, протекающий через его поверхность. В альтернативном подходе Лагранжа изменения свойств некоторого жидкого элемента фиксируется наблюдателем, движущемся вместе с этим элементом. В представленных задачах гидродинамические процессы удобнее описывать с точки зрения Эйлера.

В декартовой системе координат, где u, v, w – компоненты скорости по осям x, y, z, уравнение (2.1.1) принимает вид:

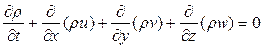. (2.1.4)

Заметим, что уравнение (2.1.4) записано в форме закона сохранения (дивергентной форме) весьма удобной для учета особенностей численного моделирования сложных течений в трубах с особенностью границ области движения рабочего тела. Рассмотрим формы записи уравнения (2.1.1) для моделей вязких сред. Напомним, что жидкость, плотность которой остается постоянной, называется несжимаемой. Математически это означает, что

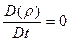. (2.1.5)

Тогда уравнение (2.1.3) будет сведено к уравнению:

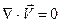, (2.1.6)

а в декартовой системы координат имеем:

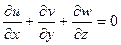. (2.1.7)

Перейдем к уравнениям движения.