Современные методы и модели исследования сложных сдвиговых потоков

1.1. Тенденции в моделировании гидродинамики и тепломассообмена при ламинарных и турбулентных течениях в трубопроводах. Из библиографических источников, учебной и специальной литературы, посвященных механике жидкости и газа, вычислительной гидродинамике хорошо известно, что одним из наиболее простых случаев движения вязкой несжимаемой жидкости в трубопроводах, трубах и каналах является ламинарное течение. При таком течении линии тока представляют собой плавные прямые линии, определяемые видом твердых границ, ограничивающих движение среды. Как показывают опыты, такое движение осуществляется в трубах с различными формами поперечных сечений, если только число Рейнольдса Re не превосходит некоторого своего критического значения Re_кр. В противном случае движение перестает быть ламинарным и частицы среды перемещаются по сложным неустойчивым траекториям нестационарного потока. При дальнейшем увеличении скорости течения в трубах формируется вихревой режим сложного сдвигового потока – турбулентный. В таком движении поля скоростей, давлений, температур и других величин имеют весьма сложную структуру. Из-за наличия в потоке турбулентных неоднородностей, “пятен” структура потока чувствительна к мгновенным случайным пульсациям поля давления, скорости и температуры. В таких условиях параметры среды становятся иррегулярными как по пространству, так и по времени. Причем детальный эксперимент позволяет обнаружить, что пространственно-временные масштабы этих неоднородностей существенно превосходят соответствующие масштабы молекулярных движений. Поэтому описание турбулентных течений с помощью дифференциальных уравнений законов сохранения импульса, тепла и массы вполне оправдано. Заметим, что имеются определенные достижения в вопросах прямого численного моделирования турбулентных течений по уравнениям, записанным для мгновенных значений искомых величин. Однако широкое использование такого подхода невозможно из-за значительных сложностей технического характера. Кроме того, существуют определенные трудности принципиального характера, не позволяющие провести полное описание турбулентных движений.

В настоящее время в расчетах сложных сдвиговых течений с пространственной и тепловой деформацией потока в технических приложениях (например, в трубопроводах) все большую популярность приобретает альтернативный метод, базирующийся на полуэмпирической теории турбулентности и включающий многопараметрические модели для моментов второго порядка. Наряду с относительно простыми двухпараметрическими моделями современные модели с транспортными уравнениями для компонент полного тензора напряжений Рейнольдса и турбулентных потоков тепла и массы представляют мощное направление в детальном изучении сложных процессов. Однако они сложны в реализации и нуждаются в предварительной оценке своих возможностей на ряде конкретных режимов работы технических устройств. В практике прикладных задач двухпараметрические тепловые и динамические модели турбулентности в сравнении с многопараметрическими выглядят предпочтительнее из-за широты области приложений, полноты апробаций, но не лишены трудностей в описании существенно анизотропных процессов без соответствующей модификации к конкретным условиям, например, внезапному отрыву потока из-за скачка площади поперечного сечения, наличия переходов и т. д. Поэтому исследования механизмов отрыва, присоединения, ламинаризации или турбулизации потока, а именно эти процессы сопровождают течение среды при его продвижении по трубопроводу, весьма актуальны. Стоит заметить так же, что в условиях численного расчета течений с ламинарно-турбулентным переходом очень высока степень доверия вычислительному алгоритму, поэтому анализу турбулентного тепло- и массообмена должна предшествовать кропотливая работа по предсказанию предельных устойчивых ламинарных режимов. Эти данные являются хорошим материалом для оценки эффективности подхода, надежности метода к описанию сложного сдвигового течения с интенсивным тепло- и массообменом в технических устройствах.

Представляется целесообразным остановиться на отдельных работах, посвященных современному моделированию процессов переноса импульса, тепла и массы в каналах. В учебном смысле такой опыт в анализе широкого круга проблем, связанных с формулировкой задач и выбором метода и методик их решения для любого специалиста весьма полезен и важен. Отметим, что библиография вопросов расчета теплообмена в каналах и трубопроводах достаточно широко представлена в отечественных и зарубежных изданиях. В настоящее время имеются решения многих задач о теплообмене и сопротивлении при вынужденной, свободной и смешанной конвекции, исследованы закономерности течения и теплообмена в трубах, проанализировано влияние на гидродинамику и теплообмен переменных свойств жидкости, достигнуты существенные успехи в численном решении полных уравнений движения (уравнений Навье-Стокса) и энергии для двумерных течений, однако, по-прежнему актуальны задачи о гидродинамики и теплообмене в сложных устройствах, трубопроводах с особенностью границ области течения углеводородных сред. Анализ этих данных позволяет заключить, чтов настоящее время теория теплопроводности достигла высокого уровня и известной завершенности, дает возможность решать практически любую задачу для изотропных неоднородных систем. Для решения нелинейных задач, задач со сложной геометрией, при наличии других осложняющих обстоятельств инженеры прибегают к численным методам решения с применением ПЭВМ. При этом обычно используются метод конечных разностей [1] и/или метод контрольного объема [2].

В качестве предмета дальнейших исследований по указанному направлению представляют большой интерес общие задачи о теплообмене при ламинарных течениях. К ним относятся двух- и трехмерные стационарные и нестационарные задачи, в том числе и сопряженные. Для обработки и интерпретации опытных данных, получаемых в сложных условиях, важны обратные задачи теплообмена (в том числе теплопроводности). Решение этих и других задач требует усовершенствования численных методов и использования ПЭВМ с большим объемом памяти и высоким быстродействием. Указанные работы подчеркивают необходимость строгой математической физики задач о ламинарном течении и теплообмене. Их решение связано с преодолением преимущественно математических трудностей и в большинстве случаев может быть проверено с необходимой точностью. Следовательно, при получении опыта в анализе сложных течений знания в моделировании более простых ламинарных течений весьма полезны. Необходим опыт исследований ламинарных потоков с высокой степенью достоверности, опираясь на существующий эксперимент, с целью возможного обобщения численных методик на более сложные турбулентные процессы.

Выше мы отмечали, что в настоящее время прямое численное моделировании (ПЧМ) возможно только для потоков с относительно низкими числами Рейнольдса. Однако метод ПЧМ очень полезен для описания турбулентной структуры, так как способен дать полную информацию о картине течения и участвовать в оценке эффективности турбулентных моделей. В результате решения проблем, связанных с интегрированием уравнений Навье - Стокса методами ПЧМ, получил развитие метод крупных вихрей (МКВ), в котором масштабы движения, большие размеров ячейки, рассчитываются непосредственно из уравнений, а мелкомасштабные – подлежат моделированию тем или иным способом.

В настоящее время при рассмотрении статистических осредненных полей искомых характеристик широкое распространение получил моментный подход, а также метод использования приближенных эмпирических соотношений и предположений чисто эвристического характера, достоверность которых не вызывает сомнения в ряде частных случаев. В отличие от МКВ, статистические модели турбулентности охватывают весь спектр турбулентных масштабов течения.

В рамках моментного подхода можно выделить три основных способа моделирования турбулентности. Два используют понятие вихревой вязкости, в котором турбулентные напряжения Рейнольдса 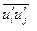предполагаются пропорциональными градиентам средней скорости с коэффициентом пропорциональности 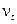(вихревая вязкость), определяющим интенсивность турбулентного обмена. Третий подход основан на непосредственном определении напряжений Рейнольдса из дифференциальных уравнений и известен в литературе, как полная схема замыкания на уровне моментов второго порядка. Модели первых двух типов составляют модели: нулевого порядка, одно-, двухпараметрические, к третьему относятся многопараметрические модели переноса рейнольдсовых напряжений (ПРН).

Использование коэффициента вихревой вязкости позволяет строить решения, пригодные лишь в конкретных условиях. Сложные турбулентные движения, часто встречающиеся в инженерных приложениях, требуют использования более общих приемов в моделировании. Практические потребности в изучении сдвиговых течений способствовали формированию тенденции к построению технологичных моделей турбулентного переноса, содержащих транспортные уравнения для одноточечных корреляционных моментов второго, третьего порядка, а также отдельные уравнения для двухточечных моментов, и позволили перейти от глубоко эмпирических подходов к ПРН-­моделям, в сущности полуэмпирическим. Такие модели существенно более надежны при изучении явлений в системах и устройствах со сложной геометрией, а также в процессах, осложненных круткой потока. Недостаточная апробация таких моделей определяет необходимость их широкого тестирования. Заинтересованных данными вопросами следует направить к работам B.Е. Launder, К. Hanjalic, W. Rodi, R.M.C. Sо, S. Elghobashi, N. Shima, В.А. Коловандина, А.Ф. Курбацкого, Э.П. Волчкова, Ю.В. Лапина, внесшим большой вклад в изучение этих проблем. Анализ показывает, что с точки зрения создания надежных численных методик большинство из моделей не выглядят универсальными. Проблема конструирования многопараметрических моделей сопряжена с расширением банка экспериментальных данных, содержащих сведения о структуре турбулентности, которые в настоящее время противоречивы.

С академической точки зрения (для большей ясности решения инженером-вычислителем вопроса выбора модели, метода, алгоритма и перспектив их реализации на практике) целесообразно также кратко указать детали построения сложных многопараметрических моделей.

1.2. Этапы построения сложных моделей с учетом анизотропии.Основа современных ПРН-моделей была заложена в работах Дж.К. Ротты, П.Я. Чоу, В.И. Давыдовым, К.Р. Дональдсоном, К.У. Хиртом, Б.Дж. Дэйли, Ф.Х. Харлоу. Эти исследования убедили, что трудности численного решения всех транспортных нелинейных дифференциальных уравнений в частных производных для компонент тензора турбулентных напряжений вполне преодолимы и замыкание определяющих течение осредненных уравнений технически возможно. В настоящее время ведется активная работа по усовершенствованию первых версий ПРН-моделей, что, в конечном счете, должно завершиться созданием универсальной и надежной основы для расчета широкого спектра течений, содержащих, в частности, искривление линий тока, отрыв, закрутку, рециркуляционные зоны и т.д. Этот уровень замыкания действительно обеспечивает большую гибкость и позволяет создать модели, применимые в широких пределах изменения определяющих параметров.

В настоящее время некоторые из моделей уже приобретают черты, характерные для нового этапа в проведении такого рода работ. Уже сейчас имеются результаты, позволяющие судить об эволюции рейнольдсовых напряжений в развивающемся сдвиговом течении. Но такое течение представляется существенно анизотропным. Поэтому необходим подход, учитывающий этот фактор.

Анизотропный характер турбулентности оказывает решающий вклад в баланс процессов, определяющих изменение осредненного импульса, тепла и массы, и требует пристального изучения. Как показывает опыт, в среде, турбулизированной естественным образом, наблюдается анизотропия процессов переноса. Поэтому анализ напряженного состояния такой среды целесообразно проводить с привлечением связей, учитывающих процессы энергетического обмена в искомых напряжениях. Такими связями могут быть полные уравнения для 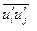, выражающие взаимодействия между процессами конвекции 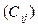, порождения 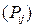, диффузии 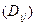, перераспределения 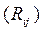и диссипации 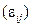и имеющие следующую структуру:

. (1)

Данный подход (замыкание на уровне вторых моментов) есть основа моделирования сложных двух- и трехмерных течений с эффектами тепломассопереноса. Тестирование таких моделей лучше начинать с изотермического случая. Поэтому первоначально должны быть рассмотрены проблемы моделирования турбулентного переноса импульса.

В пособии рассматриваются так называемые сложные турбулентные течения. К ним относятся часто встречающиеся в технике инертные и химически реагирующие закрученные потоки. До настоящего времени в таких задачах (например, о смешении внутренних закрученных струй) применялись только модели турбулентности типа вихревой вязкости. Были предприняты значительные усилия, направленные на преодоление недостатков моделей скалярной вязкости, главными из которых являются большие погрешности расчетных значений размера и интенсивности рециркуляционной зоны в сильно закрученных потоках и невозможность расчета при помощи различных двухпараметрических моделей наблюдаемого в эксперименте течения, сформированного комбинацией свободного и вынужденного вихрей. В ряду двухпараметрических моделей особенно популярна -модель У.П.Джонса – Б.Е. Лаундера главным образом благодаря своей простоте и малым затратам ресурсов ЭВМ при ее реализации. Действительно, многие прямоточные течения, в частности пограничные слои, струи, движения в каналах с химическими реакциями, с успехом рассчитываются на базе -моделей [3]. Несостоятельность -моделей в случае внутренних закрученных течений обусловлена скорее всего ущербностью допущения об изотропном характере турбулентного переноса. В свое время Д.Г. Лилли и Н.А. Чигер показали, что в сильнозакрученных потоках вихревая вязкость не может рассматриваться в виде скалярной характеристики. Модификации 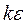-модели, учитывающие эту анизотропию, значительно улучшают точность расчетов, но, не обладая универсальностью, они не годятся для расчета трехмерных течений. Не так давно были предприняты попытки модификации 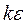-моделей посредством учета демпфирующего влияния стенок, с тем, чтобы их можно было применять для сквозного расчета пристеночных течений. Уязвимым для критики звеном является здесь набор постоянных, вводимый для учета воздействия стенок, который необходимо всякий раз подбирать в зависимости от вида течения и величины числа 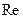. Эти трудности при применении 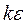-моделей неизбежны.

В связи с наличием отмеченных недостатков 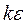-моделей и вообще моделей вихревой вязкости целесообразно обратить внимание на работы по моделированию крупных вихрей, а также по использованию моделей переноса рейнольдсовых напряжений. В таких моделях турбулентные напряжения находят из решения соответствующих модельных балансовых уравнений, представляющих собой уравнения в частных производных. При этом существенно увеличивается время расчетов. Это связано с необходимостью дополнительного интегрирования по крайней мере еще шести уравнений. Более простые модели с алгебраическими соотношениями для напряжений (АМН), которые описывают анизотропию без вышеуказанных издержек, смогут в ряде случаев служить промежуточным звеном между 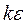-моделью и моделью переноса рейнольдсовых напряжений (ПРН). Отметим, что применение АМН-моделей имеет успех в расчетах тонких сдвиговых слоев, не осложненных эффектами сильной крутки. К настоящему времени известно лишь несколько приложений ПРН-моделей к расчету закрученных течений. В основном они относятся к струям, где их применение также не обошлось без проблем. В связи со сказанным необходимо оценить перспективность ПРН-моделей, актуальность разработки и применения алгебраических АМН-моделей для расчета внутренних течений с закруткой и без нее.

Некоторые результаты последних исследований российских ученых стоит отметить, учитывая большой вклад отечественной школы в вопросы теоретического и экспериментального моделирования турбулентности. Такие исследования разнообразны благодаря огромному числу технических приложений. Литература по этому вопросу исключительно обширна.

В числе указанных направлений, активно развиваемых с конца XX века, весьма заметны работы, выполненные Б.В.Алексеевым, А.М. Липановым, О.М. Белоцерковским, Ю.В. Лапиным, М.Х. Стрельцом, А.Ф. Курбацким, Б.П.Головней и др.

Работами Б.В. Алексеева положено начало оригинальному подходу анализа турбулентности с кинетических позиций, являющихся развитием идей Больцмана. В классическом понимании турбулентность с характерной для нее иррегулярностью изменения теплогидродинамических параметров и широким диапазоном масштабов пульсирующих величин описывается навье-стоксовской моделью. Недостатки такой модели течения связаны с отсутствием в них колмогоровских флуктуаций и, следовательно, определяющие уравнения проблематично считать уравнениями, записанными относительно истинных величин. В этом смысле полученные на основе уравнения Больцмана Б.В. Алексеевым обобщенные гидродинамические уравнения (ОГУ) являются более совершенными и универсальными, так как явно учитывают в спектре пульсаций колмогоровские флуктуации и позволяют моделировать вихревые течения в широком диапазоне чисел Re, включая режимы ламинарно-турбулентных переходов.

Несмотря на привлекательность и новизну идей описания турбулентности уравнениями Б.В. Алексеева (ОГУ), вопросы разрешимости этих уравнений еще слабо изучены и пока нет уверенности в возможностях применения данного подхода для решения практических задач. Как всякая новая теория она отвергает уже устоявшиеся представления о том, что уравнения Навье-Стокса являются теоретической базой для описания турбулентности. Однако, как всегда бывает в таких случаях, после продолжительных споров по этому поводу явно встанет тяжелый вопрос о границах применимости ОГУ и уравнений Навье-Стокса.

В прямом численном моделировании на основе полных уравнений Навье-Стокса значительные успехи достигнуты А.М. Липановым, О.М. Белоцерковским. Расчеты при больших числах Re (до 10⁵) для трехмерного канала со скачком площади поперечного сечения на входе с использованием весьма малых шагов по пространству и времени, а также схем высокого порядка точности.

О.М. Белоцерковским в рамках данного направления исследован широкий класс задач о свободных турбулентных течениях в струях, следах с эффектами отрыва, ламинарно-турбулентного перехода и явлений перехода к хаосу.

В последнее время активно развивается моментный подход в механике турбулентности. Этому подходу уделяется много внимания в группах, руководимых Ю.В. Лапиным, А.Ф. Курбацким.

В теоретическом описании турбулентности одной из главных проблем является выбор моделей, методов реализации численных алгоритмов, создание устойчивых численных схем интегрирования многомерных уравнений переноса, конструирование подходящих разностных сеток. По этим вопросам получены новые результаты, в частности, разработана оригинальная трехпараметрическая ( 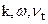)- модель турбулентности и метод ориентированной псевдоконвекции. Достоинства последнего связаны с простотой и экономичностью расчета установившихся и нестационарных пространственных течений с высокими числами Re и Pe за счет оригинального представления конвективного переноса конечно-разностной аппроксимацией второго порядка точности.

Представленный материал показывает, что математические методы решения задач тепло- и массообмена при турбулентных внутренних течениях по существу такие же, что и при ламинарных. Однако вследствие большей сложности исходной системы уравнений здесь значительно чаще используется численные методы. Необходимо отметить, что в изучении теплообмена при турбулентных течениях в трубах и каналах, пограничных слоях, свободных и пристеночных течениях в последние годы достигнуты значительные успехи [4]. Тем не менее, существует настоятельная необходимость развивать и совершенствовать методы расчета турбулентных течений, изучать новые вопросы, возникающие в различных областях. Небольшой экскурс в историю вопроса показывает, что исследование теплообмена при турбулентном движении жидкости в трубах начались около ста лет назад и первой работой, анализирующей эту проблему, была статья Нуссельта. В этой работе, посвященной теплообмену при турбулентном течении газа в трубах, впервые применен метод подобия для обобщения опытных данных по теплообмену. В последующие годы были проведены многочисленные экспериментальные исследования процессов теплообмена при турбулентном течении в трубах различных жидкостей и газов. В результате этих исследований выявлена зависимость чисел Нуссельта от чисел Рейнольдса и Прандтля в широком диапазоне изменения последних ( 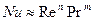, где n, m – некоторые постоянные отвечающие конкретной рабочей среде). Первая попытка теоретического рассмотрения вопроса о теплообмене при турбулентном течении жидкости в трубах принадлежит Рейнольдсу.

В реальных условиях физические свойства жидкости зависят от температуры. Поэтому закономерности теплообмена, полученные в предположении о постоянстве физических свойств, можно использовать на практике либо при небольших разностях температур в потоке, либо при слабом изменении физических свойств в рассматриваемом диапазоне температур. В этих случаях влияние изменения физических свойств можно приближенно учесть, выбрав свойства при некоторой средней температуре среды.

Заметим, что в энергетических системах, обеспечивающих эффективный транспорт рабочего тела по каналам, часто реализуются большие температурные напоры и высокие плотности теплового потока. При этом в потоке жидкости возникают большие градиенты температуры. В качестве теплоносителей нередко используются жидкости и газы, физические свойства которых весьма сильно изменяются в зависимости от температуры. Анализ движения жидкости и теплообмен в подобных условиях необходимо проводить с учетом зависимости физических свойств жидкости от температуры. Кроме того, для различных веществ и для одного и того же вещества в разных областях параметров состояния характер изменения физических свойств с температурой и давлением различен. При современном уровне знаний описать закономерности движения жидкости и теплообмена в этих разнообразных условиях с помощью единых зависимостей не представляется возможным. Вследствие этого задача о движении жидкости распадается на ряд задач, каждая из которых соответствует определенному типу зависимости физических свойств от температуры и давления.

На пути расчетно-теоретического исследования движения жидкости и теплообмена при переменных физических свойствах возникают значительные трудности математического и физического характера. Математические трудности состоят в нелинейности уравнений движения и энергии в случае переменности теплофизических свойств. Однако эти трудности преодолимы, например, путем использования численных методов решения уравнений и применения вычислительных машин.

Применение теоретических методов к исследованию турбулентных течений и процессов тепло- и массообмена гораздо более сложно, а положение в этой области менее удовлетворительно. В описании таких процессов необходимо располагать уравнениями для расчета турбулентных напряжений 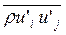, турбулентных тепловых потоков 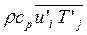и турбулентных потоков массы 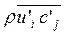. При современном уровне развития теории турбулентности эти уравнения не могут быть получены в достаточно общей и строгой форме. В последнее время в анализе турбулентного тепло- и массообмена в трубопроводах достигнут значительный прогресс в изучении структуры пристеночного внутреннего течения. Выявлено существование выбросов замедленной жидкости из вязкого подслоя в турбулентное ядро и вторжение ускоренной жидкости в область ламинарного подслоя, изучены многие детали такого течения. Дальнейшее изучение представленной структуры течения, закономерностей переноса импульса, тепла и массы в пристеночной области позволит более обоснованно аппроксимировать неизвестные члены в уравнениях для вторых моментов, придать большую универсальность вводимым функциям и постоянным. Стоит заметить, что отдельные оригинальные идеи моделирования ложных сдвиговых течений с помощью моделей ПРН-потоки можно найти, например, в [5].

Кроме того, поскольку большинство пространственных течений в трубопроводах сопровождаются влиянием массовых сил, например, вращения, то это может приводить к любопытным процессам, которые требуют некоторого искусства при моделировании. Дадим некоторые пояснения существа вращающихся потоков и проблем построения вычислительных алгоритмов подобных течений.

1.3. Характеристика закрученных потоков. Хорошо известно, что закрутка потока в зависимости от назначения промышленных устройств, трубопроводов, вихревых камер позволяет получать в них интенсифицированные (газотурбинные системы, теплообменники) или ослабленные (гидро- и аэроциклоны, сепараторы) процессы турбулентного переноса. В настоящее время основные усилия по изучению закрученных течений в нефтяном секторе сосредоточены на анализе интегрального влияния крутки на характер течения химически активных продуктов по трубопроводу. Известно, что структура течения в канале с высокой степенью закрутки потока весьма сложна, существенно отличается от структуры осевого и влияет на распределение коэффициента вихревой вязкости и касательных напряжений. Информация о турбулентных характеристиках вращающихся течений в каналах является более ограниченной по сравнению с данными о средних скоростях течения. Имеющиеся в литературе сведения теоретического и экспериментального характера часто дают только качественные представления об умеренно закрученном потоке в длинных трубах, тогда как для практики более интересны случаи сильно закрученного течения на коротком отрезке трубы. В последних - тангенциальная составляющая скорости W соизмерима или больше осредненной осевой скорости 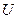. Их особенностью является возникновение зоны интенсивного обратного тока среды вблизи оси симметрии (или стенки) и высокая степень турбулентности (или ламинаризация). Такие течения мало изучены. В частности, отсутствуют данные о структуре турбулентности в широком диапазоне изменения параметров крутки и других условий течения. В силу этого в настоящее время для расчета характеристик движения и теплообмена во внутренних закрученных потоках используются эмпирические уравнения, полученные в условиях, отвечающих определенному характеру начальной крутки. Эти уравнения не универсальны, поскольку при обобщении опытных данных применялись параметры, не характеризующие гидродинамическое подобие внутренних потоков. В то же время существующие методы расчета аэродинамики и тепломассообмена базируются на конкретных предположениях о структуре турбулентности, требующих экспериментальной проверки.

Отличительные особенности закрученного течения в коротких трубах можно установить и объяснить, зная закономерности распределения полей осредненных скоростей, давления и пульсационных характеристик. Известно, что при относительно малых величинах тангенциальной составляющей скорости частицы жидкости во всех точках сечения трубы будут только удаляться от начального сечения, однако с ростом значений окружных скоростей такая форма движения становится неосуществимой и при интенсивной закрутке поступающей в трубу среды в ядре потока возникает зона возвратного течения. В этом случае жидкость движется в определенном направлении только по периферии, тогда как в центральной части осевые составляющие скорости направлены в противоположную сторону. Таким образом, можно говорить о двух характерных зонах в поле течения: кольцевая периферийная зона, через которую протекает практически вся жидкость и внутренняя приосевая зона нулевого расхода, которая представляет ядро закрученного течения. Следует отметить, что параметры потока в периферийной области весьма консервативны по отношению к возмущениям, приходящим из ядра течения. Возникновение рециркуляционного ядра обусловлено затуханием вращательного движения жидкости и увеличением давления у оси трубы по мере удаления жидких частиц от начального сечения. Поэтому определение характера затухания крутки по длине канала и нахождение зависимости радиуса рециркуляционного ядра от степени крутки потока являются важными с практической точки зрения вопросами.

Размеры и расположение зон обратных токов определяют важные характеристики трубопроводных систем: трение, теплообмен. Для того, чтобы научиться правильно управлять работой таких устройств, необходимо детально исследовать особенности закрученного течения. Поэтому в настоящее время при изучении течений в трубопроводах все шире используется математическое моделирование со сложными моделями турбулентности.

Наличие крутки потока, входящего в трубопровод, осложняет и без того непростой характер течения хотя бы тем, что создает сдвиговый слой с интенсивным перемешиванием между компонентами. Крутка оказывает влияние на эффективность смешения, на распределение температуры в области течения и характер образования различного рода загрязняющих веществ. В этих условиях понятна актуальность создания успешных методик расчета внутренних реагирующих течений как при наличии крутки, так и без нее. Основой расчета представляющих практический интерес реагирующих потоков может являться адекватная модель турбулентности, дополненная эффективной моделью химического взаимодействия. Такие модели должны точно описывать не только процессы турбулентного переноса количества движения, массы и тепла, но и правильно описывать кинетику химических реакций. Все эти моменты важны для расчетов процессов в нефте- и газопроводах. Для некоторых приложений переносы массы и энергии являются более важными в сравнении с переносом количества движения. Однако в трубопроводах вряд ли можно отделить тепловую часть задачи от динамической.

В то же время применение моделей, ориентированных на представление только количества движения (например, в задаче с тепломассообменом в предположении постоянства турбулентных чисел Прандтля и Льюиса), во многих важных случаях также оказывается необоснованным.

Во введении мы постарались кратко коснуться особенностей математического моделирования прямоточных и закрученных инертных и химически реагирующих течений. Учитывая большую практическую значимость вопросов комплексного физико-математического моделирования сложных течений в трубопроводах и ограниченность объема данного учебного пособия, интересующиеся могут обратиться к специальным источникам, например, [6], обсуждающим в деталях проблемы предсказания тепломассообмена в трубопроводах в условиях устойчивого и переходного ламинарно-турбулентного течения. Перейдем к сути математической формулировки процессов гидродинамики и теплообмена в замкнутых системах.