Глава 4. Технология численного решения гидродинамических задач

4.1. Обзор методов и алгоритмов решения определяющих уравнений.Для простоты изложения особенностей моделирования сложного сдвигового течения воспользуемся декартовой системой и предположением, что поток двухмерный. В этих условиях система определяющих уравнений будет иметь вид.

Уравнение неразрывности:

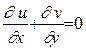. (4.1)

Уравнения движения в проекциях на оси Ox, Оу соответственно:

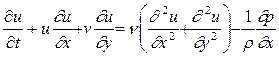; (4.2)

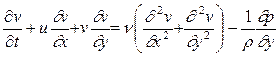. (4.3)

где ν - кинематическая вязкость.

Основная трудность численного интегрирования системы (4.1) – (4.3) (определения поля скорости) связана с определением поля давления. Градиент давления составляет часть источникового члена в уравнении количества движения, при этом нет явного уравнения для определения давления. При заданном поле давления решение уравнений количества движения не представляет собой сложности. Однако способ нахождения поля давления не очевиден. Поэтому в пособии алгоритмам его нахождения уделяется особое внимание. Отметим отдельные подходы, дающие возможность обойти эту проблему. В их числе известны методы, основанные на решении уравнения для вихря. Онипривели к возникновению методик, основанных на решении уравнений, получаемых при исключении давления из системы определяющих уравнений. При этом в нашем случае (постановки для двухмерных задач) исключение давления из двух уравнений количества движения путем перекрестного дифференцирования каждого уравнения будет приводить к уравнению переноса вихря. Вместе с введением функции тока для стационарных двухмерных течений этот метод является основой широко известного метода решения в переменных функция тока – вихрь, описанного, например, в [9].

Подход с использованием завихренности и функции тока в качестве независимых переменных является одним из распространенных методов решения двумерных уравнений Навье - Стокса для несжимаемой жидкости. Суть в следующем. Делают замену переменных, переходя от компоненты скорости к завихренности 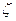и функции тока .

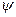В декартовых двухмерных координатах 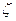определяется как:

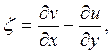(4.4)

а 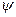определяется как:

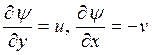. (4.5)

Используя новые независимые переменные, два уравнения движения (4.2) и (4.3) можно скомбинировать, исключая давление, что дает вид:

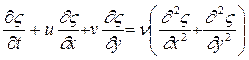. (4.6)

Это параболическое уравнение с частными производными называется уравнением переноса завихренности. Затем, подставив (4.4) в (4.5), получают дополнительно уравнение для независимых переменных эллиптического типа:

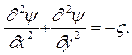(4.7)

Это эллиптическое уравнение с частными производными является уравнением Пуассона.

В результате такой замены переменных осуществляется разделение смешанной эллиптически-параболической системы уравнений Навье-Стокса для несжимаемой жидкости на одно параболическое уравнение (уравнение переноса завихренности) и одно эллиптическое уравнение (уравнение Пуассона). Обычно эти уравнения решают методом установления по времени.

С точки зрения технологии их решения отметим, что параболические уравнения переноса вихря и эллиптические уравнения Пуассона естественно рассматривать по отдельности, так как методы их решения, очевидно, различны. Однако сразу следует заметить, что при численном решении задачи гидродинамики фактически существует обратная связь между этими уравнениями. Например, в силу того, что эти уравнения решаются циклически, увеличение допустимых временных шагов для уравнения переноса вихря должно быть компенсировано увеличением числа итераций при итерационном решении уравнения Пуассона. Неправильное обращение с граничными условиями в одном уравнении может привести к нарушению сходимости в другом. Еще важнее то обстоятельство, что приходится явно искусственно отделять нахождение решения во внутренних точках от расчета граничных условий, так как обе эти процедуры должны выполняться совместно.

Окончательный выбор метода решения уравнения переноса вихря зависит от многих факторов. Таких, как: 1) граничные условия; 2) геометрия задачи; 3) тип искомого решения (стационарный или зависящий от времени); 4) возможная необходимость расчета поля температуры; 5) при решении нестационарной задачи важен выбор интервала изменения рассматриваемых параметров, в частности, числа Рейнольдса.

Рассматриваемый метод имеет несколько особенностей. Давление не входит в число зависимых переменных, и вместо того. чтобы иметь дело с двумя уравнениями количества движения и уравнением неразрывности, необходимо решить только два уравнения для нахождения функции тока – вихря. Некоторые из граничных условий записываются достаточно просто: если к расчетной области примыкает внешнее безвихревое течение (вихрь на границе удобно положить равным нулю). Однако метод решения в переменных функция тока – вихрь имеет серьезные недостатки. Условие для вихря на стенке задать трудно, и это часто осложняет получение сходящегося решения. Давление, которое было так успешно исключено из формулировки задачи, часто оказывается искомым конечным результатом решения или промежуточным результатом, необходимым для расчета плотности и других теплофизических, молярных и других свойств жидкости. В этих случаях трудности, возникающие при определении давления по полю вихря, компенсируют преимущества использования переменных функция тока – вихрь. Кроме того, основным недостатком метода является невозможность использования его в случае трехмерных задач, для которых не существует функции тока. Но большинство практических задач трехмерны, поэтому метод, ограниченный двумя измерениями, сильно проигрывает от этого существенного ограничения.

В трехмерном случае при введении вихря в качестве независимой переменной формулировка гидродинамической части задачи будет включать шесть независимых переменных, а именно, три составляющие вихря и три составляющие вектора потенциала скорости. Таким образом, задача оказывается сложнее, чем при использовании непосредственно трех составляющих скорости и давления. Введение вектора вихря и вектора потенциала скорости вместо составляющих скорости и давления менее наглядно.

В качестве одного из первых методов решения уравнений Навье - Стокса для несжимаемой жидкости, записанных относительно примитивных переменных, был предложен метод искусственной сжимаемости. В этом методе в уравнение неразрывности включен член с искусственной сжимаемостью, который обращается в нуль, когда решение устанавливается во времени. При этом уравнения Навье - Стокса образуют смешанную систему гиперболических и параболических уравнений, которая решается методом установления. Остановимся кратко на подходах этого направления к определению поля скорости.

4 .1.1. Алгоритм SIMPLE.

Алгоритм, разработанный для расчета поля течения, получил название SIMPLE(Semi-Implicit Method for Pressure-Linked Equations), что означает полунеявный метод для связывающих давление уравнений. Данный алгоритм описывался в [2].

Дискретизация (получение конечно-разностного аналога исходной системы дифференциальных уравнений) про­изводится методом контрольного объема. Основная идея метода контрольного объема легко по­нятна и поддается прямой физической интерпретации. Так, расчетная область разби­вается на некоторое конечное число непере­секающихся контрольных объемов таким образом, что каждая узловая точка содержится в одном контрольном объеме. Дифференциальное уравнение интегрируется по каждому из контрольных объемов. Для вы­числения интегралов используются кусочные профили, которые описывают изменение переменноймежду узловыми точками. В результате получается дис­кретный аналог дифференциальных урав­нений, в который входят значения пере­менной в некоторых узловых точках.

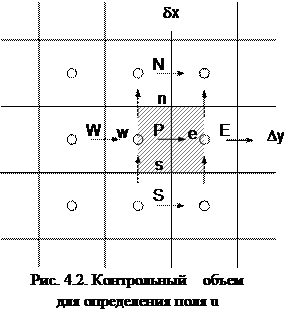
Полученный подобным образом дискретный аналог выражает закон сохранения для конечного контрольного объема точно так же, как дифференциальное уравнение выражает закон сохранения для бесконечно малого контрольного объема. Одним их важных свойств метода контрольного объема является то, что в нем заложено точное интегральное сохранение таких величин, как масса, количество движения и энергия на любой группе контрольных объемов и, следовательно, на всей расчетной области [2]. Это свойство проявляется при любом числе узловых точек, а не только в предельном случае очень большого их числа. Таким образом, даже решение на грубой сетке удовлетворяет точным интегральным балансам. Ниже приведены геометрии контрольных ячеек вокруг узла P (рис.4.1) и ячеек к расчету поля скорости (рис.4.2, 4.3). Причем символы w,n,e,s характеризуют “стороны света”, значения коэффициентов диффузии в конечно-разностных уравнениях.

Заметим, что перед применением метода контрольного объема для получения дискретизации исходной системы, строиться шахматная сетка. Исходная область 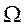покрывается равномерной сеткой .

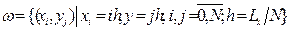	Кроме того, видно, что давление определяется в узловых точках построенной сетки, а компоненты скорости определяются в точках расположенных на гранях контрольного объема. Таким образом, строится шахматная сетка. Все достоинства выбора именно такой сетки описаны в [2, 5, 6]. Теперь перейдем к получению конечно–разностного аналога для дифференциальной системы уравнений.

Рассмотрим дифференци­альное уравнение переноса:

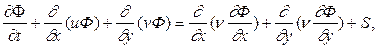(4.8)

где 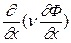, 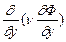- диффу­зионные члены, 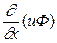, 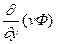- конвективные,

S – источниковый член.

y

х

Если вместо Ф подставлять соот­ветственно u, v, то из уравнения (4.8) можно получить уравнения движения для соответствующих компонент скорости.

Интегрирование уравнения (4.8) по контрольному объему дает:

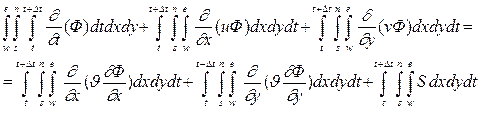; (4.9)

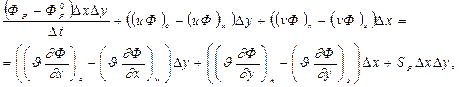(4.10)

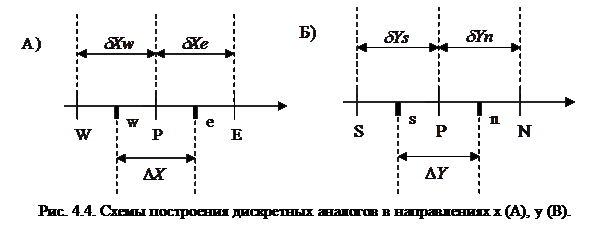
где 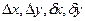- величины, показанные на рис. 4.4.

Если в уравнении (4.10) заменить производные, присутствующие в диффузионных членах на их центрально-разностные аналоги вида:

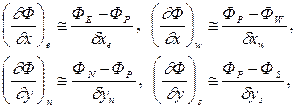(4.11)

а затем ввести обозначения:

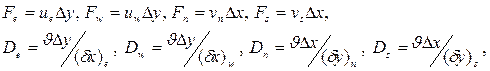(4.12)

то уравнение (4.10) примет вид:

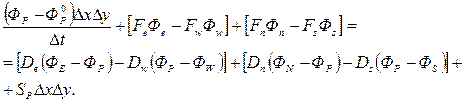(4.13)

Аналогичным образом можно проинтегрировать уравнение неразрыв­ности

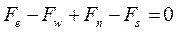. (4.14)

Если умножить уравнение (4.14) на 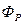и вычесть результат из уравнения (4.13) то получится уравнение:

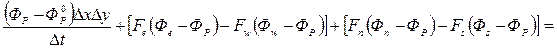
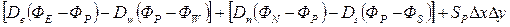. (4.15)

Здесь использованы следующие обозначения:

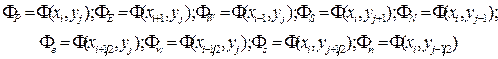
Выбор формул для определения значений Ф на гранях контрольного объема зависит от выбора схемы для аппроксимации конвективных членов. При использовании обычной схемы против потока (UPWIND) значение функции на грани контрольного объема полагается равным значению функции в узле, находящемся с «подветренной» стороны (рис. 4.5).

, ,

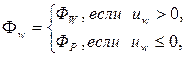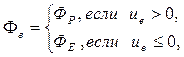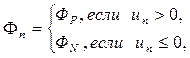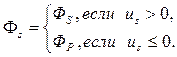, (4/16)

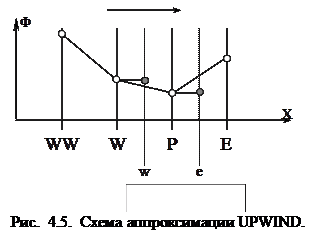Как нетрудно выяснить, построенные таким образом схемы являются схемами первого порядка. Результаты расчетов по таким схемам показывают проявление схемной вязкости, изменяющей картину течения [9]. Схемная вязкость проявляется в сглаживании резких, скачкообразных изменений функции Ф за счет возникновения искусственной диффузии при использовании схемы против потока.

Используя (4.16), выражение (4.15) можно представить в следующем виде.

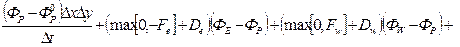
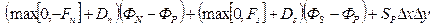. (4.17)

Если ввести следующие обозначения:

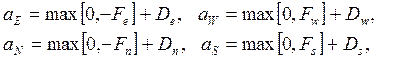
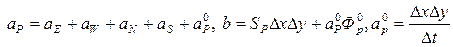, (4.18)

то тогда (4.17) можно записать в следующем виде:

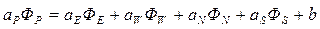. (4.19)

Дискретные аналоги для определения компонент скорости u и v в соот­ветствующих контрольных объемах (см. рис. 4.2, 4.3) имеют вид:

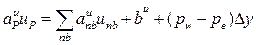; (4.20)

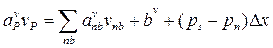. (4.21)

Значения коэффициентов a_nb, a_p связаны с влиянием совместных кон­вективных и диффузионных процессов на гранях контрольного объема и имеют вид, аналогичный (4.18) с учетом смещения контрольного объ­ема.

Уравнения движения можно решить только в том случае, если поле давления задано или каким-либо образом найдено. Если при реше­нии использовалось некорректное поле давления, найденное поле скорости не бу­дет удовлетворять уравнению неразрывности. В этом случае поле скорости, получаемое с использованием приближенного поля давления р^*, выразим через u^* u v^* и найдем из решения системы уравнений:

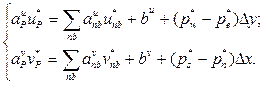(4.22)

Существует способ улучшения получения приближенного поля р^* таким образом, чтобы результирующее поле скорости с каждой итерацией лучше удовле­творяло уравнению неразрывности. Представим, что истинное давление может быть найдено из соотношения 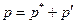, где 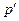- поправка давления. Необходимо установить, как будут изменяться составляющие скорости в соответствии с таким изменением давления. Для этой цели введем поправки скорости 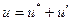, , 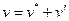где 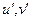- добавки к скоростям на коррекцию. Вычитая из уравнений системы (4.20, 4.21) уравнения (4.22), а также пренебрегая членами 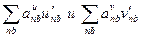, можно получить поправочные формулы для скорости:

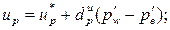(4.23)

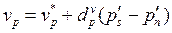, (4.24)

где .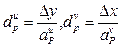

Интегрируя уравнение неразрывности по контрольному объему, можно получить его дискретный аналог в виде уравнения для поправки дав­ления, если вместо составляющих скорости подставить их выражения из поправочных формул для скорости:

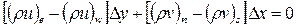, (4.25)

где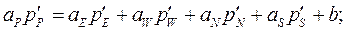

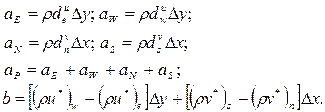(4.26)

Из (4.26) можно видеть, что член b в уравнении для поправки давления по существу равен левой части дискретного аналога уравнения неразрывно­сти (4.14), записанного через значения составляющих скорости с индексом *. Равенство b=0 означает, что эти составляющие удовлетворяют уравне­нию неразрывности и не требуется никакой коррекции давления. Таким об­разом, член b представляет собой «источник массы», который должен быть скомпенсирован поправкой давления.

Таким образом, для нестационарного случая алгоритм SIMPLE Патанкара-Сполдинга можно представить в виде следующей последовательности этапов [2]:

1. Представления начального поля давления p^о и задания p^*= p^о, t=0.

2. Определения начального поля скорости u^o, v^o.

3. Решение уравнений движения для получения u^*, v^*.

4. Решение уравнения для 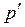(4.25) и расчет р путем добавления 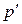к p^*.

5. Нахождение u, v с помощью формул для поправки скорости (4.23), (4.24).

6. В случае , если | 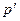| мало во всех узлах расчетной сетки, то полагаем p^о= p, u^o=u, v^o=v, t=t+Dt. В противном случае используем найденное p как p^* и переходим к этапу п.3.

7. Если t < T_max, то имеем возврат к п. 3.

Процедура SIMPLE с успехом была использована для решения целого ряда задач расчета течений несжимаемой жидкости. Однако в некоторых случаях скорость сходимости оказывается недостаточно быстрой. Это связано с тем, что уравнение для поправки давления дает завышенные значения, даже если соответствующие поправки к компонентам скорости вполне правдоподобны. Поэтому уравнение 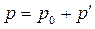часто заменяют уравнением 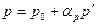, где 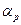- параметр нижней релаксации. Поскольку сразу невозможно определить оптимальное значение параметра нижней релаксации, процедуру SIMPLE модифицируют с целью увеличения скорости сходимости. Такая модифицированная процедура получила название SIMPLER (SIMPLE revised) [2,6]. В ней поправки к скорости вычисляются так же, как и в процедуре SIMPLE, но используется полное уравнение Пуассона для давления. Кроме того, сначала приближенно задается поле скорости, а не поле давления. Поскольку в таких условиях вычисляемое в процедуре SIMPLER давление близко к корректному искомому, то необходимость в нижней релаксации становится существенно ниже. В результате этого сходимость решения достигается за меньшее число итерации.

4.1.2. Конечно-разностные методы расчета внутренних течений.Конечно-разностные методы особенно пригодны в анализе развивающихся течений на участках от области непосредственного входа до зоны условно развитого течения. В настоящее время хорошо известно [8, 10, 11], что в общем случае движения сложного потока по каналу полной стабилизации не существует. Напомним, что гидродинамически стабилизированным мы называем течение в котором распределение скорости в поперечном сечении статистически равнозначно и не меняется в осевом направлении. В условиях движения полностью развитого простого сдвигового потока метод конечных разностей не играет большой роли, так как в этом случае уравнения в частных производных могут быть сведены к обыкновенным дифференциальным уравнениям. Примером такого движения при вязкостном режиме течения выступает широко известное течение Хагена– Пуазейля.

Заметим, что особенностью расчета стационарных и нестационарных внутренних течений является задание при постановке задачи о течении расхода жидкости через любое сечение, перпендикулярное оси канала, Это дополнительное соотношение позволяет использовать эффективные и быстродействующие маршевые методы с оригинальными методиками нахождения поля давления при численном решении уравнений движения. Одной из таких методик выступает подход Л.М. Симуни [12]. .