Глава 3. Основные уравнения турбулентного течения и теплообмена в каналах
Полученная выше система дифференциальных уравнений в более компактном тензорном виде применительно к турбулентному течению, включающая уравнения неразрывности, динамические уравнения Рейнольдса, энергии имеет вид:
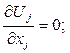 (3.1)
(3.1)
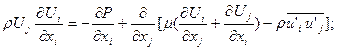 (3.2)
(3.2)
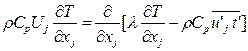 . (3.3)
. (3.3)
Здесь осреднение ведется по Рейнольдсу. Согласно Рейнольдсу, можно представить мгновенные значения скорости, температуры и других величин в виде суммы средних и пульсационных величин:
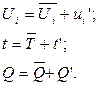 (3.4)
(3.4)
Появляющиеся из-за нелинейности исходных уравнений дополнительные неизвестные 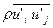 и
и 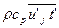 всецело связаны со случайными процессами в турбулентном потоке. Эти члены означают появление дополнительного турбулентного трения и дополнительного переноса субстанции в потоке, вызываемых пульсациями скорости. Число неизвестных в системе уравнений становится больше числа уравнений, и система оказывается незамкнутой. Это обстоятельство составляет главную трудность теоретического изучения процессов турбулентности. Поэтому основная проблема турбулентности заключается в отыскании строгих статистических соотношений, позволяющих замкнуть систему уравнений.
всецело связаны со случайными процессами в турбулентном потоке. Эти члены означают появление дополнительного турбулентного трения и дополнительного переноса субстанции в потоке, вызываемых пульсациями скорости. Число неизвестных в системе уравнений становится больше числа уравнений, и система оказывается незамкнутой. Это обстоятельство составляет главную трудность теоретического изучения процессов турбулентности. Поэтому основная проблема турбулентности заключается в отыскании строгих статистических соотношений, позволяющих замкнуть систему уравнений.
В том, что такие соотношения в природе существуют, сомнения нет, так как в противном случае не существовали бы устойчивые средние значения скорости и температуры, то есть не происходило бы физического замыкания системы уравнений. В настоящее время наука еще далека от полного решения проблемы турбулентности. Поэтому широкое распространение получили полуэмпирические теории и методы в исследовании процессов турбулентности, выражающие тем или иным способом связь между пульсационными и усредненными характеристиками и замыкающие таким образом систему уравнений.
Во введении отмечались достоинства различных подходов и методов. Подчеркнем, что для практики очень эффективна феноменологическая теория турбулентности. По одной из ее классификаций все модели турбулентного переноса мы представили группами:
1. Группа моделей турбулентной вязкости 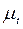 .
.
2. Модели, связанные с использованием полных транспортных уравнений переноса вторых моментов пульсации скорости и пульсаций скаляра.
Укажем наиболее распространенные в приложениях модели из каждой группы. Так, к группе моделей турбулентной вязкости относятся следующие.
3.1. Нульпараметрические модели. В этих моделях используются только алгебраические выражения для коэффициентов молярного переноса импульса и тепла. Наиболее известная среди моделей этого класса модель пути смешения Прандтля:
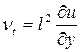 , (3.5)
, (3.5)
где l=ǽy, ǽ=0.4 (константа Кармана). Здесь l – длина пути смешения, универсальна для пристеночной зоны движении у гладкой поверхности.
3.2. Однопараметрические модели.В этих моделях используется дифференциальное уравнение, как правило, для молярной вязкости 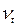 , либо кинетической энергии K. Эта группа моделей, в которых имеется возможность учета предыстории развития явлений переноса и интенсивности пульсационного движения. Уравнение переноса турбулентности – это уравнение кинетический энергии, которое в общем случае пространственного теч6ения имеет вид:
, либо кинетической энергии K. Эта группа моделей, в которых имеется возможность учета предыстории развития явлений переноса и интенсивности пульсационного движения. Уравнение переноса турбулентности – это уравнение кинетический энергии, которое в общем случае пространственного теч6ения имеет вид:
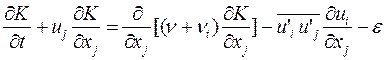 . (3.6)
. (3.6)
В условиях переменности теплофизических свойств в (3.6) неизвестными могут являться кинематическая вязкость 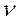 и молярная вязкость
и молярная вязкость 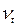 . Если имеется задача учета размера вихря, то вместо скорости диссипации
. Если имеется задача учета размера вихря, то вместо скорости диссипации 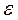 вводится, согласно теории размерности, связь:
вводится, согласно теории размерности, связь:
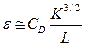 , (3.7)
, (3.7)
где L – характерный масштаб энергосодержащих вихрей.
В отношении L для погранслойных течений удовлетворительна эмпирическая связь Прандтля-Никурадзе:
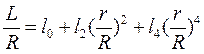 , (3.8)
, (3.8)
где в отношении коэффициентов li используются значения:
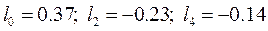 . (3.9)
. (3.9)
Однопараметрические модели основаны на концепции об изотропном характере процессов переноса импульса тепла и массы. Согласно этому положению из теории размерности следует соотношение Колмогорова-Прандтля для вязкости:
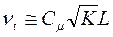 . (3.10)
. (3.10)
Тензор напряжений Рейнольдса связан с тензором скоростей деформации соотношением Буссинеска:
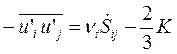 . (3.11)
. (3.11)
Недостаток однопараметрической модели связан с отсутствием представлений об изменении второй характеристики вихревого движения от времени и пространства в отличии от кинетической энергии.
3.3. Двухпараметрические модели.Вэти модели входят дифференциальные уравнения для величин определяющих интенсивность переноса вихря и его размер (группа моделей K – ε, K—L). В таких моделях важным является учет большого фактора общей динамичности нежели в моделях нулевого и первого порядка.
K – ε моделиимеют вид [5,6]:
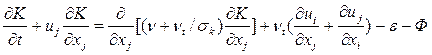 ;(3.12)
;(3.12)
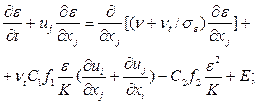 (3.13)
(3.13)
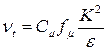 , (3.14)
, (3.14)
где в отношении 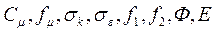 используются связи:
используются связи:
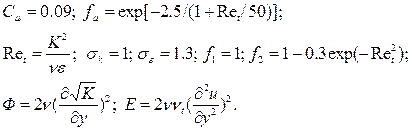 (3.15)
(3.15)
Заметим, что введение последних двух слагаемых в (3.12), (3.13) связано с численными проблемами – постановкой граничных условий на стенке типа 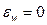 ,
, 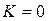 . Связи (3.12) – (3.15) работают как для моделей с высокими числами
. Связи (3.12) – (3.15) работают как для моделей с высокими числами 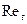 так и при малых значениях в широком диапазоне изменения осредненных величин.
так и при малых значениях в широком диапазоне изменения осредненных величин.
Популярность K – ε модели турбулентности, различных ее модификаций вызвана в основном удовлетворительным качественным описанием исследуемых процессов. Однако известно, что K – ε модель по существу неспособна воспроизвести большой максимум в распределении кинетической энергии турбулентности. С этой точки зрения K—L модель выглядит несколько предпочтительнее [5]. Кроме того, она более экономична при построении стационарных решений.
Основу K—L модели турбулентности составляют уравнения баланса кинетической энергии турбулентности K и выбранное по работам Г.С. Глушко [7] уравнения для масштаба турбулентности L, которые в случае течения несжимаемого газа в цилиндрической системе координат имеют вид [5,8]:
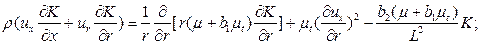 (3.16)
(3.16)
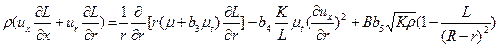 . (3.17)
. (3.17)
Значения констант 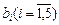 можно найти в [5].
можно найти в [5].
В вышеуказанных главах мы кратко рассмотрели основные положения в моделировании реальных систем, обладающих динамикой. Как видно, на этом этапе известными выступают законы, управляющие поведением системы. Однако их непосредственное использование часто оказывается затруднительным. Ниже пойдет речь идет как о подходах и методах решения определяющих уравнений, так и о вычислительных трудностях, связанных с отсутствием информации, содержащейся в решении точных уравнений и путях ее получения для решения вопроса о замыкании системы. Кроме того, видно, что первый шаг в построении математической модели связан с формулировкой модели явления на основе физических законов и их формализации математическим языком. Перейдем к краткой характеристике основных понятий физико-математического моделирования и технологии решения задач.
Дата добавления: 2020-07-18; просмотров: 744;











